
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE. 
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
【答案】
(1)解:如图所示,连接BO,
∵∠ACB=30°,
∴∠OBC=∠OCB=30°,
∵DE⊥AC,CB=BD,
∴Rt△DCE中,BE= ![]() CD=BC,
CD=BC,
∴∠BEC=∠BCE=30°,
∴△BCE中,∠EBC=180°﹣∠BEC﹣∠BCE=120°,
∴∠EBO=∠EBC﹣∠OBC=120°﹣30°=90°,
∴BE是⊙O的切线;
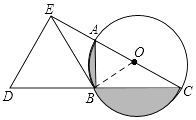
(2)解:当BE=3时,BC=3,
∵AC为⊙O的直径,
∴∠ABC=90°,
又∵∠ACB=30°,
∴AB=tan30°×BC= ![]() ,
,
∴AC=2AB=2 ![]() ,AO=
,AO= ![]() ,
,
∴阴影部分的面积=半圆的面积﹣Rt△ABC的面积= ![]() π×AO2﹣
π×AO2﹣ ![]() AB×BC=
AB×BC= ![]() π×3﹣
π×3﹣ ![]() ×
× ![]() ×3=
×3= ![]() ﹣
﹣ ![]()
【解析】(1)连接BO,根据△OBC和△BCE都是等腰三角形,即可得到∠BEC=∠OBC=∠OCB=30°,再根据三角形内角和即可得到∠EBO=90°,进而得出BE是⊙O的切线;(2)在Rt△ABC中,根据∠ACB=30°,BC=3,即可得到半圆的面积以及Rt△ABC的面积,进而得到阴影部分的面积.
【考点精析】关于本题考查的扇形面积计算公式,需要了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)平移后的三个顶点坐标分别为:.A1( ),B1( ),C1( ).
(2)在上图中画出平移后三角形A1B1C1;
(3)画出△AOA1并求出△AOA1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点. 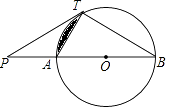
(1)求证:PT2=PAPB;
(2)若PT=TB= ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)CD与EF平行吗?并说明理由;
(2)若∠A=72°,求∠FEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F. 
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB和CD与直线MN相交.
(1)如图①,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足________时,AB∥CD;
(2)如图②,EG平分∠MEB,FH平分∠DFE(平分的是一对同位角),则∠1与∠2满足________时,AB∥CD;
(3)如图③,EG平分∠AEF,FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB∥CD?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα= ![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
(1)【问题解决】
请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ![]() ,求sin2β的值.
,求sin2β的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com