
【题目】如图所示,直线AB和CD与直线MN相交.
(1)如图①,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足________时,AB∥CD;
(2)如图②,EG平分∠MEB,FH平分∠DFE(平分的是一对同位角),则∠1与∠2满足________时,AB∥CD;
(3)如图③,EG平分∠AEF,FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB∥CD?请说明理由.

【答案】(1)∠1+∠2=90°;(2)∠1=∠2;(3)∠1=∠2,理由详见解析.
【解析】
(1)根据角平分线定义得出∠BEF=2∠1,∠DFE=2∠2,∠1+∠2=90°时,求出∠BEF+∠DFE=180°,根据平行线的判定推出即可.
(2)根据角平分线定义得出∠BEM=2∠1,∠DFE=2∠2,求出∠BEM=∠DFE,根据平行线的判定推出即可.
(3)根据角平分线定义得出∠AEF=2∠1,∠DFE=2∠2,求出∠AEF=∠DFE,根据平行线的判定推出即可.
解:(1)∠1+∠2=90°时,AB∥CD,
理由是:EG平分∠BEF,FH平分∠DFE,
∴∠BEF=2∠1,∠DFE=2∠2,
∵∠1+∠2=90°,
∴∠BEF+∠DFE=180°,
∴AB∥CD,
故答案为:∠1+∠2=90°.
(2)∠1=∠2,
理由是:EG平分∠BEM,FH平分∠DFE,
∴∠BEM=2∠1,∠DFE=2∠2,
∵∠1=∠2,
∴∠BEM=∠DFE,
∴AB∥CD,
故答案为:∠1=∠2.
(3)∠1=∠2,
理由是:EG平分∠AEF,FH平分∠DFE,
∴∠AEF=2∠1,∠DFE=2∠2,
∵∠1=∠2,
∴∠AEF=∠DFE,
∴AB∥CD.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,在△ABC内求作一点O,使点O到三边的距离相等.甲同学的作法如图1所示,乙同学的作法如图2所示,对于两人的作法,下列说法正确的是( )
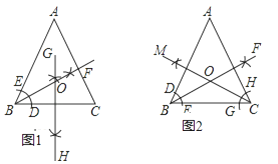
A.两人都对B.两人都不对C.甲对,乙不对D.乙对,甲不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE. 
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为6元的新商品,在商场试销发现:销售单价![]() (元/件)与每天销售量
(元/件)与每天销售量![]() (件)之间满足如图所示的关系:
(件)之间满足如图所示的关系:
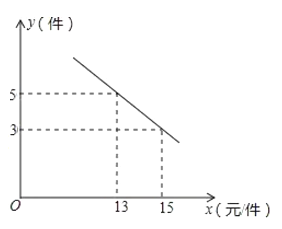
(1)求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)若你是商场负责人,要使每天的利润达到35元,应将售价定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.

请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形的圆心角为 度;
(2)将条形图补充完整;
(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有多少人呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形的操作过程:
在图①中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分);
在图②中,将折线A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影; 
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
S1= , S2= , S3= .
(3)联想与探索:
如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点D在AC上,AD=1cm,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿B→C→A的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为xcm/s.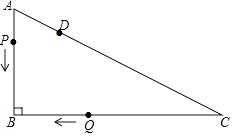
(1)点Q的速度为cm/s(用含x的代数式表示).
(2)求点P原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取 ![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com