(1)证明:由一元二次方程x
2+kx+k-1=0根的判别式,△=k
2-4(k-1)=k
2-4k+2=(k-2)
2>0,
故该抛物线与x轴有两个交点.
(2)解:设抛物线与x轴交点的横坐标为x
1,x
2,则x
1,x
2是方程x
2+kx+k-1=0的两个实根,
由根与系数的关系得x
1•x
2=k-1,
∵-1<k<1,
∴x
1x
2<0,
∴该抛物线与x轴的两个交点分别落在x轴的正负半轴上.
(3)解:存在符合条件的直角三角形.
证明:如图所示,由抛物线的对称性可知AB=BC,于是点A,B不可能为Rt△ABC的直角顶点,
∴只有点C可以为Rt△ABC的直角顶点,设点C为△ABC的直角顶点,由抛物线的对称性和

直角三角形的性质,可知AB的中点M恰是对称轴与x轴的交点,
∴CM的长为抛物线顶点的纵坐标的绝对值.
即CM=|-

|=

.
设A(x
1,0)B(x
2,0),(由(2)可知x
1<0<x
2),
则x
1,x
2是方程x
2+kx+k+1=0的两个实根,
解得x
1=-1,x
2=1-k,
∴AB=x
2-x
1=1-k+1=2-k,
由直角三角形的性质得MC=

AB,
∴

=
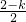
,
∵-1<k<1,
则2-k>0,
∴
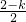
=1,
解得k=0,
∴当k=0时存在以C为直角顶点的直角三角形,
故存在符合条件的直角三角形.
分析:(1)令y=0即x
2+kx+k-1=0,根据元二次方程根的判别式,△>0,即可得出该抛物线与x轴有两个交点.
(2)根据一元二次方程x
2+kx+k-1=0根与系数的关系,及k的取值范围可求出,两根之积的正负,判断出抛物线与x轴的交点分布情况.
(3)假设存在符合条件的直角三角形.根据抛物线的对称性可知AB=BC,于是点A,B不可能为Rt△ABC的直角顶点,只有点C可以为Rt△ABC的直角顶点,由抛物线的对称性和直角三角形的性质,可知AB的中点M恰是对称轴与x轴的交点,即CM的长为抛物线顶点的纵坐标的绝对值,根据抛物线y=x
2+kx+k-1(-1<k<1),可用k表示出顶点坐标,根据一元二次方程x
2+kx+k+1=0根与系数的关系可用k表示出两根的值,再根据直角三角形的性质及k的取值范围可求出k的值.
点评:此题比较复杂,考查的是一元二次方程与二次函数的关系,及直角三角形的性质,是中学阶段的重点也是难点.

 已知抛物线y=x2+kx+k-1(-1<k<1).
已知抛物线y=x2+kx+k-1(-1<k<1). 直角三角形的性质,可知AB的中点M恰是对称轴与x轴的交点,
直角三角形的性质,可知AB的中点M恰是对称轴与x轴的交点, |=
|= .
. AB,
AB, =
=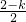 ,
,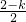 =1,
=1,

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.