
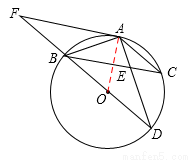
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.
(1)求证:∠ABC=∠D;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.

(1)证明见解析;(2)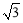 ;(3)直线FA与圆O相切,理由见解析.
;(3)直线FA与圆O相切,理由见解析.
【解析】
试题分析:(1)由AB=AC,利用等边对等角得到∠ABC=∠C,再由同弧所对的圆周角相等得到∠C=∠D,等量代换即可得证.
(2)由(1)的结论与公共角相等,得到△ABE∽△ADB,由相似得比例,即可求出AB的长.
(3)直线FA与圆O相切,理由为:连接OA,由BD为直径,得到∠BAD为直角,在直角三角形ABD中,利用勾股定理求出BD的长,得到AB=OB=OA,得到∠FBA=∠F,∠BAO=∠BOA,确定出∠OAF为直角,即可得证.
试题解析:解:(1)证明:∵AB=AC,∴∠ABC=∠C.
∵∠C与∠D都对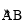 ,且在AB的同侧,∴∠C=∠D.
,且在AB的同侧,∴∠C=∠D.
∴∠ABC=∠D.
(2)∵∠ABC=∠D,∠BAE=∠DAB,∴△ABE∽△ADB. ∴ .
.
∵AE=1,ED=2,∴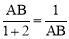 ,解得:AB=
,解得:AB=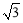 .
.
(3)直线FA与圆O相切.理由如下:
如答图,连接OA,
∵BD为圆O的直径,∴∠BAD=90°.
在Rt△ABD中,AB=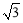 ,AD=1+2=3,
,AD=1+2=3,
根据勾股定理得:BD=2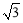 ,
,
∴OB=OA=AB=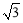 .
.
∵BF=OB,∴AB=FB=OB. ∴∠FBA=∠F,∠BAO=∠BOA.
∴∠OAF=90°.
∴直线AF与圆O相切.
考点:1.等腰三角形的性质;2.圆周角定理;3.相似三角形的判定与性质;4.切线的判定;5.勾股定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:填空题
如图,在△ABC中,AC=BC,∠B=70°,分别以点A、C为圆心,大于AC的长为半径作弧,两弧相交于点M、N,作直线MN,分别交AC、BC于点D、E,连结AE,则∠AED的度数是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:选择题
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数是( )

A.70° B.35° C.40° D.50°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:解答题
考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试. 某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类,学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”的减压方式的人数.
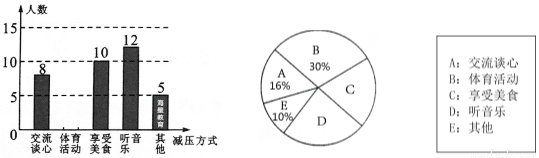
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com