
【题目】如图,已知抛物线y=![]()
![]() ﹣
﹣![]() x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
(1)、求点A和点B的坐标;
(2)、求证:四边形DECF是矩形;
(3)、连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
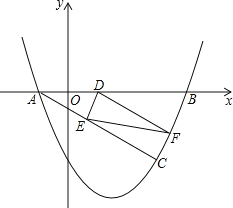
【答案】(1)、(﹣1,0),(4,0);(2)、证明过程见解析;(3)、2.
【解析】
试题分析:(1)、根据抛物线的解析式来求点A、B的坐标即可;(2)、欲证明四边形DECF是矩形,只需证得四边形DECF是平行四边形且有一内角为直角即可;(3)、连接CD,根据矩形DECF的对角线相等得到:EF=CD.当CD⊥AB时,CD的值最小,即EF的值最小.
试题解析:(1)、当y=0时,![]()
![]() ﹣
﹣![]() x﹣2=0, 解方程,得 x1=﹣1,x2=4. ∵点A在点B的左侧,
x﹣2=0, 解方程,得 x1=﹣1,x2=4. ∵点A在点B的左侧,
∴点A、B的坐标分别是(﹣1,0),(4,0);
(2)、把C(m,1﹣m)代入y=![]()
![]() ﹣
﹣![]() x﹣2得:
x﹣2得:![]() -2=1-m 解方程,得m=3或m=﹣2.
-2=1-m 解方程,得m=3或m=﹣2.
∵点C位于第四象限, ∴m>0,1﹣m<0,即m>1, ∴m=﹣2舍去, ∴m=3,
∴点C的坐标为(3,﹣2). 过点C作CH⊥AB于H,则∠AHC=∠BHC=90°.
由A(﹣1,0),B(4,0),C(3,﹣2)得到:AH=4,CH=2,BH=1,AB=5, ∴![]() =2.
=2.
又∵∠AHC=∠CHB=90°,∴△AHC∽△CHB, ∴∠ACH=∠CBH. ∵∠CBH+∠BCH=90°,
∴∠ACH+∠BCH=90°, ∴∠ACB=90°, ∵DE∥BC,DF∥AC, ∴四边形DECF是平行四边形,
∴平行四边形DECF是矩形;
(3)、存在.理由如下: 连接CD. ∵平行四边形DECF是矩形, ∴EF=CD.
当CD⊥AB时,CD的值最小. ∵C(3,2), ∴DC的最小值是2, ∴EF的最小值是2.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】计算:1+(﹣2)+(+3)+(﹣4)+(+5)+(﹣6)+…+(+99)+(﹣100)+(+101)的结果是( )
A. 0 B. ﹣1 C. ﹣50 D. 51
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_________;
(2)仔细观察,在图2中“8字形”的个数_________个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角,其他条件不变,试问∠P与∠D,∠B之间存在着怎样的数量关系(直接写出结论即可)
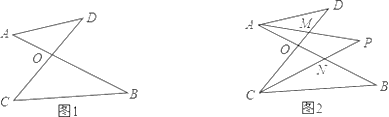
查看答案和解析>>
科目:初中数学 来源: 题型:
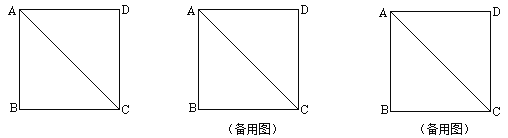
【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.
探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
①AM=CN;②∠AME=∠BNE;③BN﹣AM=2;④S△EMN=![]() .
.
上述结论中正确的个数是( )
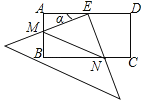
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com