
 ≈1.41,
≈1.41,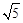 ≈2.24)
≈2.24)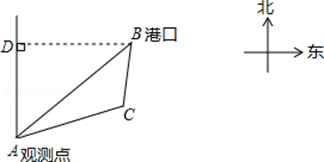
 =10。
=10。
 ,sin53.2°≈0.8,
,sin53.2°≈0.8, 。
。 ,0.5=
,0.5= ,AH=2BH。
,AH=2BH。 , AH=8
, AH=8 。
。 )2+CH2=102,解得CH=2
)2+CH2=102,解得CH=2 。
。 -2
-2 =6
=6 ≈13.4。
≈13.4。 ,得出AB的长,从而得出tan∠BAH=
,得出AB的长,从而得出tan∠BAH= ,求出BH的长,即可得出AH以及CH的长,从而得出答案。
,求出BH的长,即可得出AH以及CH的长,从而得出答案。

科目:初中数学 来源:不详 题型:解答题
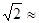 1.414,
1.414,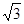 ≈1.732)
≈1.732)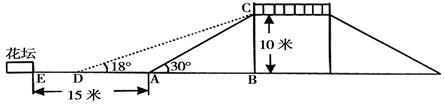
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
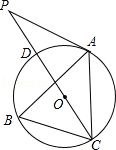
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
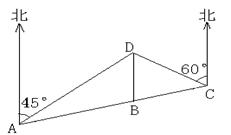
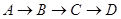 的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西
的线路输送天然气,某测绘员测得D市在A市东北方向,在B市正北方向,在C市北偏西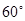 方向。C市在A市北偏东
方向。C市在A市北偏东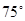 方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据:
方向。B、D两市相距20km,问天然气从A市输送到D市的路程是多少?(结果保留整数,参考数据: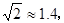
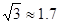 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
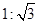 (即AB:BC=
(即AB:BC=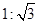 ),且B、C、E三点在同一条直线上。请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条直线上。请根据以上条件求出树DE的高度(测倾器的高度忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com