练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将下列各数填入相应的集合中.

    —7 , 0, ，—22, -2.55555…, 3.01, +9 ,4.020020002…，+10﹪, -2.

    无理数集合:{ }; 负有理数集合:{ };

    正分数集合:{ }; 非负整数集合:{ };

    【答案】无理数集合:{ 4.020020002…，-2 }；负有理数集合:{ —7 ，—22 ， -2.55555… }；正分数集合:{ ，3.01，+10﹪， }； 非负整数集合:{ 0， +9 }.

    【解析】

    根据数集的分类直接分类.

    根据数的分类直接把题目中数据进行分类，无理数集合:{ 4.020020002…，-2 }；负有理数集合:{ —7 ，—22 ， -2.55555… }；正分数集合:{ ，3.01，+10﹪， }； 非负整数集合:{ 0， +9 }.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值： ，其中x=2sin60°﹣（ ）﹣2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

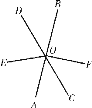
    【题目】如图，已知直线AB，CD相交于点O，OE平分∠AOD，FO⊥AB，垂足为O，∠BOD=∠DOE．

    （1）求∠BOF的度数；

    （2）请写出图中与∠BOD相等的所有的角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD位于平面直角坐标系的第一象限，B、C在x轴上A点函数上，且AB∥CD∥y轴，AD∥x轴，B（1，0）、C（3，0）。

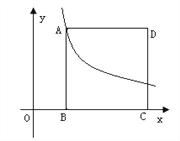
    ⑴试判断四边形ABCD的形状。

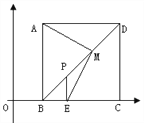
    ⑵如图若点P是线段BD上一点PE⊥BC于E，M是PD的中点，连EM、AM。

    求证：AM=EM

    ⑶在图中，连结AE交BD于N，则下列两个结论：

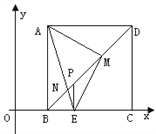
    ①值不变；②的值不变。其中有且仅有一个是正确的，请选择正确的结论证明并求其值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】世界杯比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位：m）：+10，﹣2，+5，﹣6，+12，﹣9，+4，﹣14．（假定开始计时时，守门员正好在球门线上）

    （1）守门员最后是否回到球门线上？

    （2）守门员离开球门线的最远距离达多少米？

    （3）如果守门员离开球门线的距离超过10米（不包括10米），则对方球员挑射极可能造成破门．请问在这一时间段内，对方球员有几次挑射破门的机会？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利 润捐助给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y （单位：个）与
    销售单价x（单位：元/个）之间的对应关系如图所示：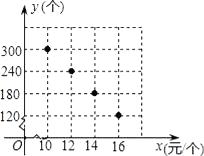

    （1）y与x之间的函数关系是 ．
    （2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（单位：元）与销售单价x（单位：元/个）之间的函数关系式；
    （3）在（2）问的条件下，若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴是一个非常重要的数学工具，它使数和数轴上的点建立对应关系，解释了数与点之间的内在联系，它是“数形结合”的基础。

    如图，数轴上有三个点A、B、C，它们可以沿着数轴左右移动，请回答

    ）

    （1）将点B向右移动4个单位长度后到达点D，点D表示的数是 ，A、D两点之间的距离是 ；

    （2）移动点A到达E点，使B、C、E三点的其中某一点到其它两点的距离相等，写出点E在数轴上对应的数值 ；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，解答下面的问题：

    我们知道方程有无数个解，但在实际生活中我们往往只需求出其

    正整数解．

    例：由，得：，（x、y为正整数）

    ∴，则有．又为正整数，则为正整数．由2与3互质，可知：x为3的倍数，从而x=3，代入∴2x+3y=12的正整数解为

    问题：

    （1）请你写出方程的一组正整数解：　　　　　　.

    （2）若为自然数，则满足条件的x值为　　　　　　.

    （3）七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根，比如对于方程 ，操作步骤是：
    第一步：根据方程系数特征，确定一对固定点A（0，1），B（5，2）;
    第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；
    第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C 的横坐标m即为该方程的一个实数根（如图1）
    第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D 的横坐标为n即为该方程的另一个实数根。

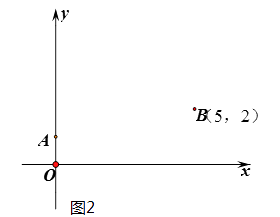
    （1）在图2 中，按照“第四步“的操作方法作出点D（请保留作出点D时直角三角板两条直角边的痕迹）
    （2）结合图1，请证明“第三步”操作得到的m就是方程 的一个实数根；
    （3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程 的实数根，请你直接写出一对固定点的坐标；
    （4）实际上，（3）中的固定点有无数对，一般地,当 ， ， ， 与a，b，c之间满足怎样的关系时，点P（ ， ），Q（ ， ）就是符合要求的一对固定点？

    查看答案和解析>>

    同步练习册答案