
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

【答案】(1)0回到球线上;(2)19米;(3)三次
【解析】试题(1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得每次与球门线的距离,根据有理数的大小比较,可得答案;
(3)根据有理数的大小比较,可得答案.
试题解析:(1)+10-2+5-6+12-9+4-14=0,
答:守门员最后正好回到球门线上;
(2)第一次10,第二次10-2=8,第三次8+5=13,第四次13-6=7,第五次7+12=19,第六次19-9=10,第七次10+4=14,第八次14-14=0,
19>14>13>10>8>7,
答:守门员离开球门线的最远距离达19米;
(3)第一次10=10,第二次10-2=8<10,第三次8+5=13>10,第四次13-6=7<10,第五次7+12=19>10,第六次19-9=10,第七次10+4=14>10,第八次14-14=0,
答:对方球员有三次挑射破门的机会.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图.请根据图中提供的信息,解答下列问题: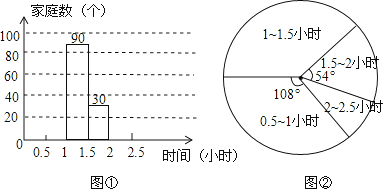
(1)本次抽样调查了多少个家庭?
(2)将图①中的条形图补充完整,直接写出用车时间的中位数落在哪个时间段内;
(3)求用车时间在1~1.5小时的部分对应的扇形圆心角的度数;
(4)若该社区有车家庭有1600个,请你估计该社区用车时间不超过1.5小时的约有多少个家庭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,AD与⊙O相切于点B,D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( ) 
A.70°
B.105°
C.100°
D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填入相应的集合中.
—7 , 0, ![]() ,—22
,—22![]() , -2.55555…, 3.01, +9 ,4.020020002…,+10﹪, -2
, -2.55555…, 3.01, +9 ,4.020020002…,+10﹪, -2![]() .
.
无理数集合:{ }; 负有理数集合:{ };
正分数集合:{ }; 非负整数集合:{ };
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1 , 设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.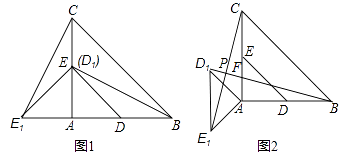
(1)如图1,当α=90°时,线段BD1的长等于 , 线段CE1的长等于;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1= CE1 , 且BD1⊥CE1;
(3)①设BC的中点为M,则线段PM的长为;②点P到AB所在直线的距离的最大值为 . (直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB和线段CD重合部分CB的长是线段AB的三分之一,M、N分别是线段AB和线段CD的中点,若![]() ,
,![]() ,则线段AD的长为________.
,则线段AD的长为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好食堂的服务工作,某学校食堂对学生最喜爱的菜肴进行了抽样调查,下面试根据收集的数据绘制的统计图(不完整):
(1)参加抽样调查的学生数是______人,扇形统计图中“大排”部分的圆心角是______°;
(2)把条形统计图补充完整;
(3)若全校有3000名学生,请你根据以上数据估计最喜爱“烤肠”的学生人数.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com