
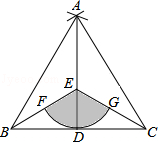
 BD=
BD= ,然后根据扇形的面积公式求解.
,然后根据扇形的面积公式求解. BD=
BD= ,
, =π.
=π.

科目:初中数学 来源:不详 题型:解答题
 PC.(不必证明)
PC.(不必证明)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
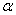 .
.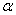 =50°,则∠1+∠2= ___________ °;
=50°,则∠1+∠2= ___________ °;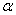 、∠1、∠2之间有何关系?
、∠1、∠2之间有何关系?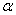 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。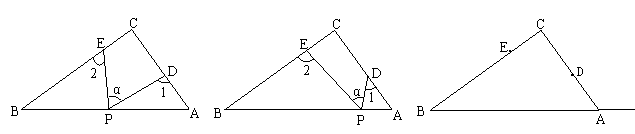
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.这种变换是相似变换 |
| B.对应边扩大到原来的2倍 |
| C.各对应角度数不变 |
| D.面积扩大到原来的2倍 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
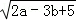 +(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
+(2a+3b﹣13)2=0,则此等腰三角形的周长为( )| A.7或8 | B.6或1O | C.6或7 | D.7或10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com