
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.
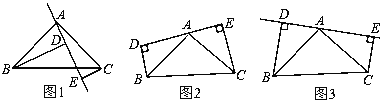
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
【答案】(1)证明见解析;(2)BD=DE+CE;(3)BD=DE+CE.
【解析】
试题分析:本题考查了全等三角形的判定和性质,涉及到直角三角形的性质、余角和补角的性质等知识点,熟练掌握全等三角形的判定方法是解题的关键.
(1)根据已知条件易证得∠BAD=∠ACE,且根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(2)BD=DE+CE.根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(3)同上理,BD=DE+CE仍成立.
试题解析:(1)在△ABD和△CAE中,
∵∠CAD+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAD=∠ABD.
又∠ADB=∠AEC=90°,AB=AC,∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.又AE=AD+DE,∴AE=DE+CE,即BD=DE+CE.
(2)BD=DE﹣CE.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.又AB=AC,∠ADB=∠CEA=90°,∴△ADB≌△CEA.∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,即 BD=DE﹣CE
(3)同理:BD=DE﹣CE.


科目:初中数学 来源: 题型:
【题目】一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形.在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个在大矩形的面积,则n的最小值是 ( )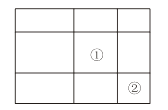
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校需要招聘一名教师,对三名应聘者进行了三项素质测试![]() 下面是三名应聘者的综合测试成绩:
下面是三名应聘者的综合测试成绩:
应聘者 成绩 项目 | A | B | C |
基本素质 | 70 | 65 | 75 |
专业知识 | 65 | 55 | 50 |
教学能力 | 80 | 85 | 85 |
(1)如果根据三项测试的平均成绩确定录用教师,那么谁将被录用?
(2)学校根据需要,对基本素质、专业知识、教学能力的要求不同,决定按2:1:3的比例确定其重要性,那么哪一位会被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节快到了,甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方法,甲旅行社的优惠方法是:买4张全票,其余人按半价优惠;乙旅行社的优惠方法是:一律按7折优惠,已知两家旅行社的原价均为每人100元。(旅游人数超过4人)
(1)分别表示出甲旅行社收费y1 ,乙旅行社收费y2与旅游人数x的函数关系式.
(2)就参加旅游的人数讨论哪家旅行社的收费更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,手机微信红包迅速流行起来.去年春节,小米的爷爷也尝试用微信发红包,他分别将10元、30元、60元的三个红包发到只有爷爷、爸爸、妈妈和小米的微信群里,他们每人只能抢一个红包,且抢到任何一个红包的机会均等(爷爷只发不抢,红包里钱的多少与抢红包的先后顺序无关).
(1)求小米抢到60元红包的概率;
(2)如果小米的奶奶也加入“抢红包”的微信群,他们四个人中将有一个人抢不到红包,那么这种情况下,求小米和妈妈两个人抢到红包的钱数之和不少于70元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(﹣2,﹣4),直线x=﹣2与x轴相交于点B,连接OA,抛物线y=﹣x2从点O沿OA方向平移,与直线x=﹣2交于点P,顶点M到点A时停止移动.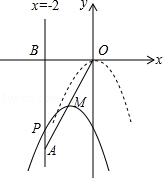
(1)线段OA所在直线的函数解析式是;
(2)设平移后抛物线的顶点M的横坐标为m,问:当m为何值时,线段PA最长?并求出此时PA的长.
(3)若平移后抛物线交y轴于点Q,是否存在点Q使得△OMQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
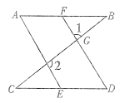
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com