
����Ŀ��ij��ľ��˾��20��������һ�������������У��ù�˾���ʻ���������������y1����䣩��ʱ��x��xΪ��������λ���죩���ֶ�Ӧֵ���±���ʾ��
ʱ��x���죩 | 0 | 4 | 8 | 12 | 16 | 20 |
����y1����䣩 | 0 | 16 | 24 | 24 | 16 | 0 |
��һ�����ʻ����Ա������ۣ�����������������y2����䣩��ʱ��x��xΪ��������λ���죩 ��ϵ��ͼ��ʾ��
��1���������ѧ����һ�κ��������κ����ͷ�����������ȷ�����ֺ����ܱ�ʾy1��x�ı仯���ɣ�д��y1��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2���۲�����������������y2��ʱ��x�ı仯���ɣ����������̼Ҳ����˺������۲���ʹ�������������˱仯����д��������y2��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��3����û�ľ��˾����������Ϊy��䣬д��y��ʱ��x�ĺ�����ϵʽ�����жϵڼ�������������y��������ʱ���ֵ�� 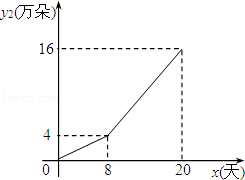
���𰸡�
��1���⣺��ͼ�����ݹ۲��֪y1��x֮���Ƕ��κ�����ϵ��
��y1=ax2+bx+c��a��0����
��  ��
��
��� 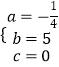 ��
��
��y1��x������ϵʽΪy1=�� ![]() x2+5x��0��x��20��
x2+5x��0��x��20��
��2���⣺����8��û�ľ��˾�����˽��۴����������������ķ����������Ա���ҵ�ע�����������������ӣ�
��0��x��8����y=kx��
�ߺ���ͼ���㣨8��4����
��8k=4��
���k= ![]() ��
��
���ԣ�y= ![]() x��
x��
��8��x��20ʱ����y=mx+n��
�ߺ���ͼ���㣨8��4������20��16����
�� ![]() ��
��
��� ![]() ��
��
���ԣ�y=x��4��
���ϣ�y2= 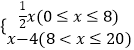 ��
��
��3���⣺��0��x��8ʱ��
y=y1+y2
= ![]() x��
x�� ![]() x2+5x
x2+5x
=�� ![]() ��x2��22x+121��+
��x2��22x+121��+ ![]()
=�� ![]() ��x��11��2+
��x��11��2+ ![]() ��
��
�������߿������£�x��ȡֵ��Χ�ڶԳ�����࣬y��x�����������
�൱x=8ʱ��y�����ֵ��y���=�� ![]() ��8��11��2+
��8��11��2+ ![]() =28��
=28��
��8��x��20ʱ��y=y1+y2=x��4�� ![]() x2+5x��
x2+5x��
=�� ![]() ��x2��24x+144��+32��
��x2��24x+144��+32��
=�� ![]() ��x��12��2+32��
��x��12��2+32��
�������߿������£�������x��ȡֵ��Χ�ڣ�
�൱x=12ʱ��y�����ֵΪ32��
��û�ľ��˾���۵�12�죬����������������ֵΪ32��䣮
����������1�����жϳ�y1��x֮���Ƕ��κ�����ϵ��Ȼ����y1=ax2+bx+c��a��0����Ȼ��ȡ�������ݣ����ô���ϵ��������κ�������ʽ��𣻣�2�����������ӣ��ӽ��۴����Ͽ��ǣ�Ȼ����������ô���ϵ������һ�κ�������ʽ��𣻣�3���֢�0��x��8ʱ����8��x��20ʱ���������������������y=y1+y2 �� �������ٸ��ݶ��κ�������ֵ������


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���B=��D=60�㣬��BAC=��ACD=90�㣬��EΪ��AB��һ�㣬AB=3AE=3cm������P��B���������1cm/s���ٶ���BC��CD��DA�˶���A��ֹͣ�����˶�ʱ��Ϊt�룮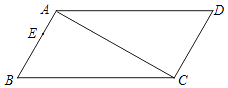
��1����֤�ı���ABCD��ƽ���ı��Σ�
��2������BEPΪ����������ʱ����t2��31t��ֵ��
��3����t=4ʱ���ѡ�ABP��ֱ��AP���ۣ��õ���AFP�����AFP��ABCD�ص����ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��F�ֱ���AD��BC���ϣ���AE=CF��
��֤����1����ABE�ա�CDF��
��2���ı���BFDE��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A ���Ӧ����Ϊ��5��B ����A ���ұߣ��������ϼס�����B�ֱ���2����λ/�롢1����λ/����ٶ������˶����������ϱ���A ��3����λ/����ٶ������˶���
��1�����������ϱ�����5���˶���C �㣬��C ���ʾ������
![]()
��2��������ͬʱ������������������1�������ң���B ���ʾ������
![]()
��3���ڣ�2���������£�������ͬʱ������ʱ��Ϊt �룬�Ƿ����t��ֵ��ʹ�����ҵľ����DZ����ľ����2���������ڣ����t ֵ���������ڣ�˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������A��ʻ��B�أ����Ը��Ե��ٶ�������ʻ���׳����ҳ�����ʻ2 h�����Ҽ׳�;����Ϣ��0.5 h����ͼ�Ǽס���������ʻ��·��y(km)��ʱ��x(h)�ĺ���ͼ����
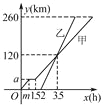
(1)���ͼ��m��a��ֵ��
(2)����׳���ʻ��·��y(km)��ʱ��x(h)�ĺ�����ϵʽ����д����Ӧ��x��ȡֵ��Χ��
(3)���ҳ���ʻ�ʱ��ʱ������ǡ�����50 km?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��BC����C����D��90�������н����в���������( )
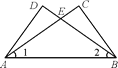
A. ��DAE����CBE B. CE��DE C. ��DAE����CBE��һ��ȫ�� D. ��1����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¶��庯������y����x�ĺ����У���0��x��1ʱ������y�����ֵ����Сֵ���ֱ��ymax��ymin �� ������ ![]() �������dzƺ���yΪ�������κ�������
�������dzƺ���yΪ�������κ�������
��1��������y=x+aΪ�������κ���������a��ȡֵ��Χ��
��2���жϺ���y=x2�� ![]() x+1�Ƿ�Ϊ�������κ���������˵�����ɣ�
x+1�Ƿ�Ϊ�������κ���������˵�����ɣ�
��3����֪����y=x2��2mx+1��������0��x��1�ϵ���������ʵ��a��b��c����Ӧ����������ֵ���ܹ���һ�������ε����߳�����������������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ���E�DZ�BC���е㣬��AEF=90������EF�����������ƽ����CF�ڵ�F�����������Ķ�����������ͼ��̽��Ƭ�Σ��������������⣮
��1��̽��1��Сǿ����ͼ��*���ܿ췢��AE=EF������Ҫ֤��AE��EF���ڵ�����������ȫ�ȣ�����ABE����ECF��Ȼ��ȫ�ȣ�һ����ֱ�������Σ�һ���Ƕ۽������Σ������ǵ���E�DZ�BC���е㣬��˿���ѡȡAB���е�M������EM������ȥ֤��AEM��EFC�����ˣ��漴Сǿд�������µ�֤�����̣�
֤������ͼ1��ȡAB���е�M������EM��
�ߡ�AEF=90��
���FEC+��AEB=90��
�֡ߡ�EAM+��AEB=90��
���EAM=��FEC
�ߵ�E��M�ֱ�Ϊ�����εı�BC��AB���е�
��AM=EC
�ֿ�֪��BME�ǵ���ֱ��������
���AME=135��
�֡�CF����������ǵ�ƽ����
���ECF=135��
���AEM�ա�EFC��ASA��
��AE=EF
��2��̽��2��Сǿ����̽������ͼ2��������������E�DZ�BC���е�����Ϊ����E�DZ�BC�ϵ�����һ�����������������䣬����AE=EF��Ȼ����������֤����һ���ۣ�
��3��̽��3��Сǿ��һ���������ԣ���ͼ3��������������E�DZ�BC���е�����Ϊ����E�DZ�BC�ӳ����ϵ�һ���������������Բ��䣬��ô����AE=EF�Ƿ�����أ��������������֤�����̸�Сǿ����������������˵�����ɣ�
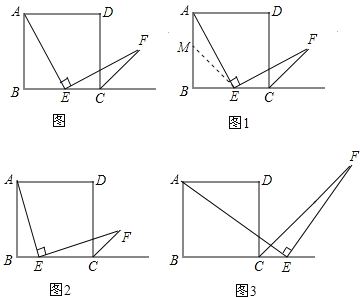
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC�У�AB=AC����BAC=120�㣬AD��BC�ڵ�D����P��BA�ӳ�����һ�㣬��O���߶�AD��һ�㣬OP=OC��
��1�����APO+��DCO�Ķ�����
��2����֤����P��OC�Ĵ�ֱƽ�����ϣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com