
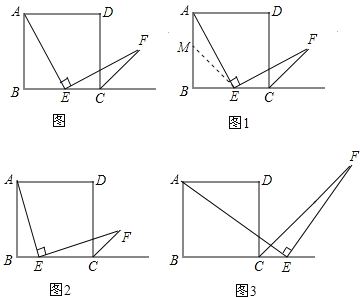
����Ŀ����ͼ���ı���ABCD�������Σ���E�DZ�BC���е㣬��AEF=90������EF�����������ƽ����CF�ڵ�F�����������Ķ�����������ͼ��̽��Ƭ�Σ��������������⣮
��1��̽��1��Сǿ����ͼ��*���ܿ췢��AE=EF������Ҫ֤��AE��EF���ڵ�����������ȫ�ȣ�����ABE����ECF��Ȼ��ȫ�ȣ�һ����ֱ�������Σ�һ���Ƕ۽������Σ������ǵ���E�DZ�BC���е㣬��˿���ѡȡAB���е�M������EM������ȥ֤��AEM��EFC�����ˣ��漴Сǿд�������µ�֤�����̣�
֤������ͼ1��ȡAB���е�M������EM��
�ߡ�AEF=90��
���FEC+��AEB=90��
�֡ߡ�EAM+��AEB=90��
���EAM=��FEC
�ߵ�E��M�ֱ�Ϊ�����εı�BC��AB���е�
��AM=EC
�ֿ�֪��BME�ǵ���ֱ��������
���AME=135��
�֡�CF����������ǵ�ƽ����
���ECF=135��
���AEM�ա�EFC��ASA��
��AE=EF
��2��̽��2��Сǿ����̽������ͼ2��������������E�DZ�BC���е�����Ϊ����E�DZ�BC�ϵ�����һ�����������������䣬����AE=EF��Ȼ����������֤����һ���ۣ�
��3��̽��3��Сǿ��һ���������ԣ���ͼ3��������������E�DZ�BC���е�����Ϊ����E�DZ�BC�ӳ����ϵ�һ���������������Բ��䣬��ô����AE=EF�Ƿ�����أ��������������֤�����̸�Сǿ����������������˵�����ɣ�
���𰸡���2��֤������������3�����������ɼ�����
�������������������2����AB�Ͻ�ȡAM=EC��Ȼ��֤����EAM=FEC����AME=��ECF=135�㣬�����á��DZ߽ǡ�֤����AEM�͡�EFCȫ�ȣ�Ȼ�����ȫ�������ζ�Ӧ����ȼ���֤����
��3���ӳ�BA��M��ʹAM=CE��Ȼ��֤����BME=45�㣬�Ӷ��õ���BME=��ECF����������ֱ��ƽ�У��ڴ������֤����DAE=��BEA��Ȼ��õ���MAE=��CEF�������á��DZ߽ǡ�֤����MAE�͡�CEFȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
�����������2��̽��2��֤������AB�Ͻ�ȡAM=EC������ME��
�ɣ�1��֪��EAM=��FEC��
��AM=EC��AB=BC��
��BM=BE��
���BME=45�㣬
���AME=��ECF=135�㣬
�ߡ�AEF=90�㣬
���FEC+��AEB=90�㣬
���ߡ�EAM+��AEB=90�㣬
���EAM=��FEC��
����AEM����EFC�� 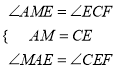 ��
��
���AEM�ա�EFC��ASA����
��AE=EF��
��3��̽��3��������
֤�����ӳ�BA��M��ʹAM=CE������ME��
��BM=BE��
���BME=45�㣬
���BME=��ECF=45�㣬
����AD��BE��
���DAE=��BEA��
���ߡ�MAD=��AEF=90�㣬
���DAE+��MAD=��BEA+��AEF��
����MAE=��CEF��
����MAE����CEF��
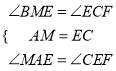 ��
��
���MAE�ա�CEF��ASA����
��AE=EF��



 �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB�ֱ�y�ᡢx����A��B���㣬OA=2��tan��ABO= ![]() ��������y=��x2+bx+c��A��B���㣮
��������y=��x2+bx+c��A��B���㣮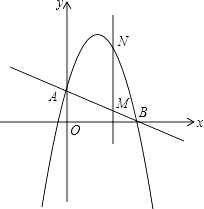
��1����ֱ��AB����������ߵĽ���ʽ��
��2���������ߵĶ���ΪD�����ABD�������
��3������ֱx���ֱ��x=t���ڵ�һ����ֱ��AB��M���������������N����tȡ��ֵʱ��MN�ij���l�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ľ��˾��20��������һ�������������У��ù�˾���ʻ���������������y1����䣩��ʱ��x��xΪ��������λ���죩���ֶ�Ӧֵ���±���ʾ��
ʱ��x���죩 | 0 | 4 | 8 | 12 | 16 | 20 |
����y1����䣩 | 0 | 16 | 24 | 24 | 16 | 0 |
��һ�����ʻ����Ա������ۣ�����������������y2����䣩��ʱ��x��xΪ��������λ���죩 ��ϵ��ͼ��ʾ��
��1���������ѧ����һ�κ��������κ����ͷ�����������ȷ�����ֺ����ܱ�ʾy1��x�ı仯���ɣ�д��y1��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2���۲�����������������y2��ʱ��x�ı仯���ɣ����������̼Ҳ����˺������۲���ʹ�������������˱仯����д��������y2��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��3����û�ľ��˾����������Ϊy��䣬д��y��ʱ��x�ĺ�����ϵʽ�����жϵڼ�������������y��������ʱ���ֵ�� 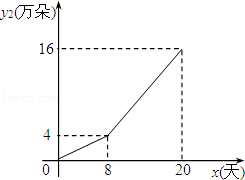
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��DE�ǹ���A��ֱ�ߣ�BD��DE��D��CE��DE�ڵ�E��
��1����B��C��DE��ͬ�ࣨ��ͼ��ʾ����AD=CE����֤��AB��AC��
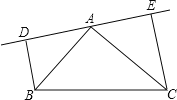
��2����B��C��DE�����ࣨ��ͼ��ʾ���������������䣬AB��AC�Դ�ֱ�����������֤���������ǣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AB�Ƕ���ΪB����y�ύ�ڵ�A��������y=��x2+4x+2��һ���֣�����BC��˫����y= ![]() ��һ���֣��ɵ�C��ʼ�����ظ���A��B��C���Ĺ��̣��γ�һ�鲨���ߣ���P��2017��m����Q��2025��n�����ڸò������ϣ�����P��Q�ֱ���x��Ĵ��ߣ�����ΪM��N������PQ�����ı���PMNQ�����Ϊ�� ��
��һ���֣��ɵ�C��ʼ�����ظ���A��B��C���Ĺ��̣��γ�һ�鲨���ߣ���P��2017��m����Q��2025��n�����ڸò������ϣ�����P��Q�ֱ���x��Ĵ��ߣ�����ΪM��N������PQ�����ı���PMNQ�����Ϊ�� �� 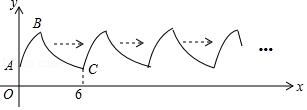
A.72
B.36
C.16
D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=�� ![]() ��ͼ����ֱ��y=kx��k��0���ཻ�ڵ�A��B����ABΪ�������������Σ�ʹ��ACB=120�㣬�ҵ�C��λ������k�IJ�ͬȡֵ�������仯������Cʼ����ijһ����ͼ���ϣ������ͼ������Ӧ�ĺ�������ʽΪ ��
��ͼ����ֱ��y=kx��k��0���ཻ�ڵ�A��B����ABΪ�������������Σ�ʹ��ACB=120�㣬�ҵ�C��λ������k�IJ�ͬȡֵ�������仯������Cʼ����ijһ����ͼ���ϣ������ͼ������Ӧ�ĺ�������ʽΪ �� 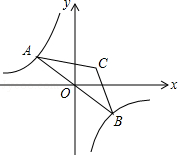
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�AE�ǡ�O��ֱ������C�ǡ�O�ϵĵ㣬����AC���ӳ�AC����D��ʹCD=CA������ED����O�ڵ�B�� 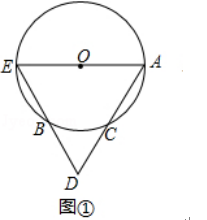
��1����֤����C���ӻ� ![]() ���е㣻
���е㣻
��2����ͼ�ڣ�����EC����AE=2AC=4������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����������BD��CE�ཻ�ڵ�F����֪��ABC=60�㣬AB=10��CF=EF�����ABC�����Ϊ�� �� 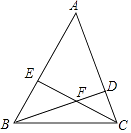
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com