
【题目】如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
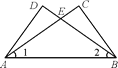
A. ∠DAE=∠CBE B. CE=DE C. △DAE与△CBE不一定全等 D. ∠1=∠2
【答案】C
【解析】题目给出的已知条件加上∠DEA=∠CEB可得△DAE≌△CBE,由全等三角形性质可得∠DAE=∠CBE,CE=DE,由AD=BC,公共边AB利用HL可以得到Rt△ABC≌Rt△BAD,根据全等三角形对应角相等可得∠1=∠2,据此对四个选项逐一进行判断即可得.
∵AD=BC,∠C=∠D=90°,∠DEA=∠CEB,∴△DAE≌△CBE,故C选项不正确,符合题意;
∴∠DAE=∠CBE,CE=DE,故A、B选项正确,不符合题意;
在Rt△ABC和Rt△BAD中,∵AD=BC, AB=BA,∴△ABC≌△ABD(HL),∴∠1=∠2,故D选项正确,不符合题意,
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形EFGH边长相等,下列说法:
①这个图案可以看成正方形ABCD绕点O旋转45°前后的图形共同组成的;
②这个图案可以看成△ABC绕点O分别旋转45°,90°,135°,180°,225°前后的图形共同组成的;
③这个图案可以看成△BOC绕点O分别旋转45°,90°,135°,225°,250°前后的图形共同组成的.
其中正确的个数有( )
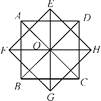
A. 1个 B. 2个 C. 3个 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式![]() x+y+1的值.
x+y+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临海市初中第三教研区为了丰富学生课余活动,组织同学开展每周一次的社团活动,活动内容有足球、跳绳、跳舞、篮球、象棋共5项,为方便组织,规定每位同学只能报一项活动,根据报名绘制了如下两幅尚不完整的统计图,解答下列问题: 
(1)将条形统计图补充完整;
(2)写出扇形统计图中的m和n的值;
(3)瑶瑶和欣欣两名同学对足球、篮球、象棋三项活动都很感兴趣,决定从三项活动中随机抽取一项参加,利用树状图或列表表示所有可能结果,并求出两人参加同一项目的概率;
(4)由于场地限制,参加足球活动的学生人数不能超过参加其余活动学生人数的 ![]() ,那么至少几位同学需要从参加足球活动调整到参加其余活动?
,那么至少几位同学需要从参加足球活动调整到参加其余活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如图所示.
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;
(2)观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;
(3)设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值. 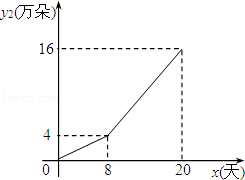
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制,0.08元/分;
(B)包月制,50元/月(限一部个人住宅电话上网);
此外,每种上网方式都附加通信费0.02元/分.
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况?如果存在,请求出这时的上网时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
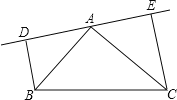
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=﹣ ![]() 的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为 .
的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为 . 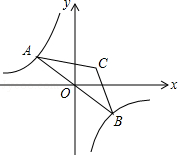
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com