
【题目】已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.

【答案】(1)见解析;(2)CB=CM+2CD.
【解析】(1)过M点作MN∥AC交AB于N,然后根据全等三角形的判定“ASA”证明△AMN≌△MHC,再根据全等三角形的性质可得MA=MH;
(2)过M点作MG⊥AB于G,再根据全等三角形的判定“AAS”证明△BMG≌△CHD可得CD=BG,因为BM=2CD可得BC=MC+2CD.
(1)如图,过M点作MN∥AC交AB于N,
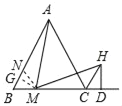
则BM=BN,∠ANM=120°,
∵AB=BC,
∴AN=MC,
∵CH是∠ACD的平分线,
∴∠ACH=60°=∠HCD,
∴∠MCH=∠ACB+∠ACH=120°,
又∵∠NMC=120°,∠AMH=60°,
∴∠HMC+∠AMN=60°
又∵∠NAM+∠AMN=∠BNM=60°,
∴∠HMC=∠MAN,
在△ANM和△MCH中,
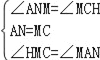 ,
,
∴△AMN≌△MHC(ASA),
∴MA=MH;
(2)CB=CM+2CD;
证明:如图,过M作MG⊥AB于G,
∵HD⊥BC,
∴∠HDC=∠MGB=90°,
∵△AMN≌△MHC,
∴MN=HC,
∵MN=MB,
∴HC=BM,
在△BMG和△CHD中,
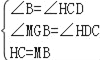 ,
,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∵△BMN为等边三角形,
∴BM=2BG,
∴BM=2CD,
∴BC=MC+2CD.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
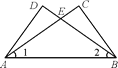
A. ∠DAE=∠CBE B. CE=DE C. △DAE与△CBE不一定全等 D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数![]() 的图像相交于点
的图像相交于点![]() 和点
和点![]() ,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 与四边形MNCA的周长相等;④
与四边形MNCA的周长相等;④![]() .其中正确的个数是( )个.
.其中正确的个数是( )个.
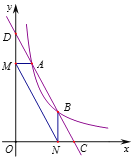
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,b)、B(a,0)、D(d,0),且a、b、d满足![]() =0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
=0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
(1)求点A、B、D的坐标;
(2)求点E、F的坐标;
(3)如图,点P(0,1)作x轴的平行线,在该平行线上有一点Q(点Q在点P的右侧)使∠QEM=45°,QE交x轴于点N,ME交y轴的正半轴于点M,求![]() 的值.
的值.
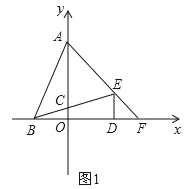

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与x轴,y轴分别交于M,N两点,且OM=ON=3.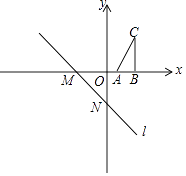
(1)求这条直线的函数表达式;
(2)Rt△ABC与直线l在同一个平面直角坐标系内,其中∠ABC=90°,AC=2 ![]() ,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.
,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( )
(x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( ) 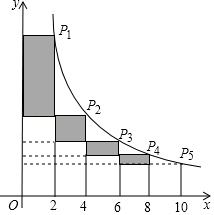
A.4.5
B.4.2
C.4
D.3.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校500名毕业生中考体育测试情况进行调查,根据男生及女生身体机能类选考坐位体前屈测试成绩整理,绘制成如下不完整的统计图(图①,图②) 
请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有人,女生有人;
(2)扇形统计图中a= , b= , 并补全条形统计图;
(3)求图①中“8分a%”所对应的扇形圆心角的度数;
(4)若该校毕业生中随机抽取一名学生,则这名男生身体机能类选考坐位体前屈测试成绩为10分的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com