
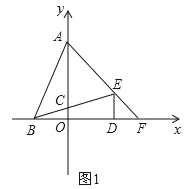
【题目】如图,在平面直角坐标系中,点A(0,b)、B(a,0)、D(d,0),且a、b、d满足![]() =0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
=0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
(1)求点A、B、D的坐标;
(2)求点E、F的坐标;
(3)如图,点P(0,1)作x轴的平行线,在该平行线上有一点Q(点Q在点P的右侧)使∠QEM=45°,QE交x轴于点N,ME交y轴的正半轴于点M,求![]() 的值.
的值.

【答案】(1)A(0,3),B(﹣1,0),D(2,0);(2)F(3,0);(3)1.
【解析】(1)由非负数的性质可求得a、b、d的值,可求得A、B、D的坐标;
(2)由条件可证明△ABO≌△BED,可求得DE和BD的长,可求得E点坐标,再求得直线AE的解析式,可求得F点坐标;
(3)过E作EG⊥OA于点G,EH⊥PQ于点Q,可证明四边形GEHP为正方形,在GA上截GI=QH,可证明△IGE≌△QHE,可证得∠IEM=∠MEQ=45°,可证明△EIM≌△EQM,可得到IM=MQ,再结合条件可求得PH=AI=PQ,可求得答案.
(1)∵![]() =0,
=0,
∴a=﹣1,b=3,d=2,
∴A(0,3),B(﹣1,0),D(2,0);
(2)∵A(0,3),B(﹣1,0),D(2,0),
∴OB=1,OD=2,OA=3,
∴AO=BD,
在△ABO和△BED中,
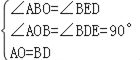 ,
,
∴△ABO≌△BED(AAS),
∴DE=BO=1,
∴E(2,1),
设直线AE解析式为y=kx+b,
把A、E坐标代入,可得
![]() ,解得
,解得![]() ,
,
∴直线AE的解析式为y=﹣x+3,
令y=0,可解得x=3,
∴F(3,0);
(3)如图,过E作EG⊥OA,EH⊥PQ,垂足分别为G、H,在GA上截取GI=QH,
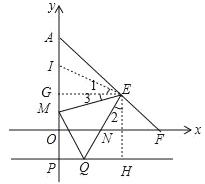
∵E(2,1),P(﹣1,0),
∴GE=GP=GE=PH=2,
∴四边形GEHP为正方形,
∴∠IGE=∠EHQ=90°,
在Rt△IGE和Rt△QHE中,
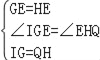 ,
,
∴△IGE≌△QHE(SAS),
∴IE=EQ,∠1=∠2,
∵∠QEM=45°,
∴∠2+∠3=45°,
∴∠1+∠3=45°,
∴∠IEM=∠QEM,
在△EIM和△EQM中,
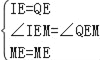 ,
,
∴△EIM=EQM(SAS),
∴IM=MQ,
∴AM﹣MQ=AM﹣IM=AI,
由(2)可知OA=OF=3,∠AOF=90°,
∴∠A=∠AEG=45°,
∴PH=GE=GA=IG+AI,
∴AI=GA﹣IG=PH﹣QH=PQ,
∴![]() =
=![]() =1.
=1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制,0.08元/分;
(B)包月制,50元/月(限一部个人住宅电话上网);
此外,每种上网方式都附加通信费0.02元/分.
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况?如果存在,请求出这时的上网时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列五个结论:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,则
;③ON⊥OM;④若AB=2,则![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正确结论是_________.(只填番号)
.其中正确结论是_________.(只填番号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线OC,将一块直角三角板的直角顶点放在O处(注:∠DOE=90°).
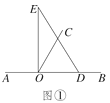

(1)如图①,若直角三角板DOE的一边OD放在射线OB上,且∠BOC=60°,求∠COE的度数;
(2)如图②,将三板DOE绕O逆时针转动到某个位置时,若恰好满足5∠COD=∠AOE,且∠BOC=60°,求∠BOD的度数;
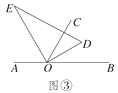
(3)如图③,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC. 
(1)求证:△BDE≌△ADC;
(2)若BC=8.4,tanC= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A(-2,6)、点B(
的图象交于点A(-2,6)、点B(![]() ,1).
,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
(3)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移n个单位,使平移后的图象与反比例函数
轴向下平移n个单位,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求n的值.
的图象有且只有一个交点,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析式为y=﹣x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(﹣1,m),且与x轴交于点A,
(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com