
【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制,0.08元/分;
(B)包月制,50元/月(限一部个人住宅电话上网);
此外,每种上网方式都附加通信费0.02元/分.
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况?如果存在,请求出这时的上网时间.
【答案】(1)A: 0.1x(元),B:50+0.02x(元);(2)54;56;(3)625分钟.
【解析】
(1)(A)计时制的费用=上网时间![]() (0.08+0.02);(B)包月制的费用=50+上网费用,把相关数值代入即可;
(0.08+0.02);(B)包月制的费用=50+上网费用,把相关数值代入即可;
(2)把x=200,300代入(1)得到的式子,计算结果比较即可;
(3)让两种费用相等,列出方程求解即可;
解:(1)A收费方式所需费用为(0.08+0.02)x=0.1x(元),
B收费方式所需费用为50+0.02x(元).
(2)当x=200时,0.1x=20,50+0.02x=54;
当x=300时,0.1x=30,50+0.02x=56.
(3)根据题意得:50+0.02x=0.1x,
解得:x=625.
答:存在625分钟时间,使得两种收费方式一样.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]() .
.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
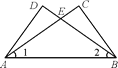
A. ∠DAE=∠CBE B. CE=DE C. △DAE与△CBE不一定全等 D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( ) 
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=![]() ,则四边形PEBF的周长为( )
,则四边形PEBF的周长为( )
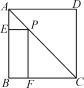
A. ![]() B. 2
B. 2![]() C. 2 D. 1
C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
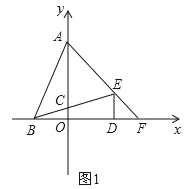
【题目】如图,在平面直角坐标系中,点A(0,b)、B(a,0)、D(d,0),且a、b、d满足![]() =0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
=0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
(1)求点A、B、D的坐标;
(2)求点E、F的坐标;
(3)如图,点P(0,1)作x轴的平行线,在该平行线上有一点Q(点Q在点P的右侧)使∠QEM=45°,QE交x轴于点N,ME交y轴的正半轴于点M,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com