
【题目】综合题。
(1)计算:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]() .
.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
【答案】
(1)解:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]()
=1+2+2 ![]()
=3;
(2)解: ![]() ÷(
÷( ![]() ﹣x+1)
﹣x+1)
= ![]()
= ![]()
= ![]() ,
,
∵﹣tan60°≤x≤2cos30°
∴ ![]() ,
,
∴当x=1时,原式= ![]() =﹣1.
=﹣1.
【解析】(1)根据零指数幂、负整数指数幂、绝对值可以解答本题;(2)先化简题目中的式子,然后根据﹣tan60°≤x≤2cos30°,从中选取使得原分式有意义的x的整数值代入即可解答本题.
【考点精析】认真审题,首先需要了解零指数幂法则(零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)),还要掌握整数指数幂的运算性质(aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数))的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=﹣2.
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究: 探究一:如图1,设△PAD的面积为S,令W=tS,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;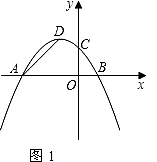
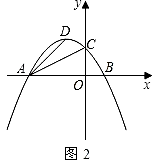
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.(参考资料:抛物线y=ax2+bx+c(a≠0)对称轴是直线x= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A1、A2、A3、…、An(n为正整数)都在数轴上.点A2在点A1的左边,且A1A2=1;点A3在点A2的右边,且A2A3=2;点A4在点A3的左边,且A3A4=3;…,点A2018在点A2017的左边,且A2017A2018=2017,若点A2018所表示的数为2018,则点A1所表示的数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:请根据图中给出的信息,解答下列问题:
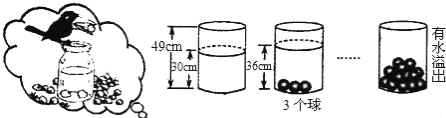
(1)放入一个小球量桶中水面升高 cm;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的函数关系式;
(3)当量桶中水面上升至距离量桶顶部3cm时,应在量桶中放入几个小球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式![]() x+y+1的值.
x+y+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
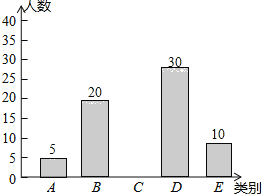
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临海市初中第三教研区为了丰富学生课余活动,组织同学开展每周一次的社团活动,活动内容有足球、跳绳、跳舞、篮球、象棋共5项,为方便组织,规定每位同学只能报一项活动,根据报名绘制了如下两幅尚不完整的统计图,解答下列问题: 
(1)将条形统计图补充完整;
(2)写出扇形统计图中的m和n的值;
(3)瑶瑶和欣欣两名同学对足球、篮球、象棋三项活动都很感兴趣,决定从三项活动中随机抽取一项参加,利用树状图或列表表示所有可能结果,并求出两人参加同一项目的概率;
(4)由于场地限制,参加足球活动的学生人数不能超过参加其余活动学生人数的 ![]() ,那么至少几位同学需要从参加足球活动调整到参加其余活动?
,那么至少几位同学需要从参加足球活动调整到参加其余活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:
(A)计时制,0.08元/分;
(B)包月制,50元/月(限一部个人住宅电话上网);
此外,每种上网方式都附加通信费0.02元/分.
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况?如果存在,请求出这时的上网时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列五个结论:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,则
;③ON⊥OM;④若AB=2,则![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正确结论是_________.(只填番号)
.其中正确结论是_________.(只填番号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com