
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=﹣2.
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究: 探究一:如图1,设△PAD的面积为S,令W=tS,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;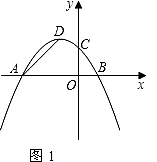
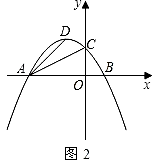
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.(参考资料:抛物线y=ax2+bx+c(a≠0)对称轴是直线x= ![]() )
)
【答案】
(1)解:∵抛物线y=ax2﹣x+3(a≠0)的对称轴为直线x=﹣2.
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∴D(﹣2,4)
(2)解:探究一:当0<t<4时,W有最大值.
∵抛物线 ![]() 交x轴于A、B两点,交y轴于点C,
交x轴于A、B两点,交y轴于点C,
∴A(﹣6,0),B(2,0),C(0,3),
∴OA=6,OC=3.
当0<t<4时,作DM⊥y轴于M,
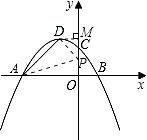
则DM=2,OM=4.
∵P(0,t),
∴OP=t,MP=OM﹣OP=4﹣t.
∵S三角形PAD=S梯形OADM﹣S三角形AOP﹣S三角形DMP
= ![]()
= ![]()
=12﹣2t
∴W=t(12﹣2t)=﹣2(t﹣3)2+18
∴当t=3时,W有最大值,W最大值=18.
探究二:
存在.分三种情况:
①当∠P1DA=90°时,作DE⊥x轴于E,
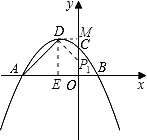
则OE=2,DE=4,∠DEA=90°,
∴AE=OA﹣OE=6﹣2=4=DE.
∴∠DAE=∠ADE=45°, ![]() ,
,
∴∠P1DE=∠P1DA﹣∠ADE=90°﹣45°=45度.
∵DM⊥y轴,OA⊥y轴,
∴DM∥OA,
∴∠MDE=∠DEA=90°,
∴∠MDP1=∠MDE﹣∠P1DE=90°﹣45°=45度.
∴P1M=DM=2, ![]() .
.
此时 ![]() ,
,
又因为∠AOC=∠P1DA=90°,
∴Rt△ADP1∽Rt△AOC,
∴OP1=OM﹣P1M=4﹣2=2,
∴P1(0,2).
∴当∠P1DA=90°时,存在点P1,使Rt△ADP1∽Rt△AOC,
此时P1点的坐标为(0,2)
②当∠P2AD=90°时,则∠P2AO=45°,
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴△P2AD与△AOC不相似,此时点P2不存在.
③当∠AP3D=90°时,以AD为直径作⊙O1,则⊙O1的半径 ![]() ,
,
圆心O1到y轴的距离d=4.
∵d>r,
∴⊙O1与y轴相离.
不存在点P3,使∠AP3D=90度.
∴综上所述,只存在一点P(0,2)使Rt△ADP与Rt△AOC相似.
【解析】(1)由抛物线的对称轴求出a,就得到抛物线的表达式了;(2)①下面探究问题一,由抛物线表达式找出A,B,C三点的坐标,作DM⊥y轴于M,再由面积关系:SPAD=S梯形OADM﹣SAOP﹣SDMP得到t的表达式,从而W用t表示出来,转化为求最值问题.②难度较大,运用分类讨论思想,可以分三种情况:(1)当∠P1DA=90°时;(2)当∠P2AD=90°时;(3)当AP3D=90°时;思路搞清晰问题就好解决了.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB,E、F、G、H分别是AB,BC,CD,AD边上的点,EG⊥FH,FH=2 ![]() ,则四边形EFGH的面积为( )
,则四边形EFGH的面积为( ) 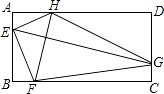
A.8 ![]()
B.8
C.12 ![]()
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.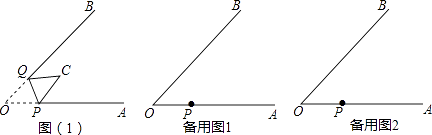
(1)当PC∥QB时,OQ=;
(2)当PC⊥QB时,求OQ的长.
(3)当折叠后重叠部分为等腰三角形时,求OQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图
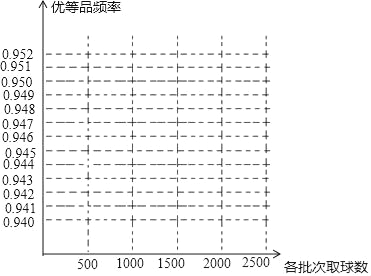
(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为![]() ,求取出了多少个黑球?
,求取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC. ①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.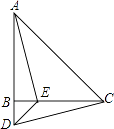
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]() .
.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com