
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.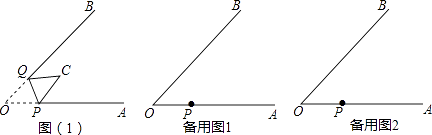
(1)当PC∥QB时,OQ=;
(2)当PC⊥QB时,求OQ的长.
(3)当折叠后重叠部分为等腰三角形时,求OQ的长.
【答案】
(1)2cm
(2)解:当PC⊥QB时,分两种情况:
(i)如图1所示:
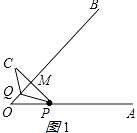
设OQ=xcm,
∵∠O=45°,
∴△OPM是等腰直角三角形,
∴OM= ![]() OP=
OP= ![]() ,
,
∴QM= ![]() ﹣x,
﹣x,
由折叠的性质得:∠C=∠O=45°,CQ=OQ=x,
∴△CQM是等腰直角三角形,
∴QC= ![]() QM
QM
∴x= ![]() (
( ![]() ﹣x),
﹣x),
解得:x=2 ![]() ﹣2,
﹣2,
即OQ=2 ![]() ﹣2;
﹣2;
(ii)如图2所示:
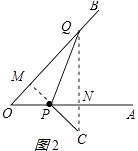
同(i)得:OQ=2 ![]() +2;
+2;
综上所述:当PC⊥QB时,OQ的长为2 ![]() ﹣2,或2
﹣2,或2 ![]() +2
+2
(3)
解:当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;
①点C在∠AOB的内部时,四边形OPCQ是菱形,OQ=OP=2cm;
②当点C在∠AOB的一边上时,△OPQ是等腰直角三角形,OQ= ![]() 或2
或2 ![]() ;
;
③当点C在∠AOB的外部时,分两种情况:
(i)如图3所示:
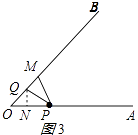
PM=PQ,则∠PMQ=∠PQM=∠O+∠OPQ,
由折叠的性质得:∠OPQ=∠MPQ,
设∠OPQ=∠MPQ=x,
则∠PMQ=∠PQM=45°+x,
在△OPM中,由三角形内角和定理得:45°+x+x+45°+x=180°,
解得:x=30°,
∴∠OPQ=30°,
作QN⊥OP于N,设ON=a,
∵∠O=45°,
则QN=ON=a,OQ= ![]() a,PN=
a,PN= ![]() QN=
QN= ![]() a,
a,
∵ON+PN=OP,
∴a+ ![]() a=2,
a=2,
解得:a= ![]() ﹣1,
﹣1,
∴OQ= ![]() (
( ![]() ﹣1)=
﹣1)= ![]() ﹣
﹣ ![]() ;
;
(ii)如图4所示:
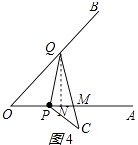
PQ=MQ,作QN⊥OA于N,
同①得:OQ= ![]() +
+ ![]() ;
;
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或(2 ![]() ﹣2,)cm或(2
﹣2,)cm或(2 ![]() +2)cm或(
+2)cm或( ![]() ﹣
﹣ ![]() )cm或(
)cm或( ![]() +
+ ![]() )cm.
)cm.
【解析】解:(1)当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
所以答案是:2cm;


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.仪征市区的公共自行车给市民出行带来不少方便.我校数学社团小学员走进小区随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况: A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.
将这次调查情况整理并绘制如下两幅统计图: 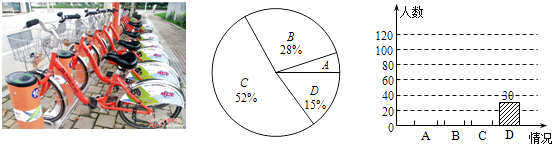
根据图中的信息,解答下列问题:
(1)本次活动共有位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若市区有26万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面各小题括号里的数,均是它前面的方程的解的是( )
A. 3x﹣1=5(2) B. ![]() +1=0(﹣5,﹣7)
+1=0(﹣5,﹣7)
C. x2﹣3x=4(4,1) D. x(x﹣2)(x+4)=0(2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE. 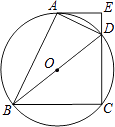
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠B=90°,∠C=30°,点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动,同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动。设点D,E的运动时间为t秒,DF⊥BC于F
(1)求证:AE=DF;
(2)如图2,连接EF,![]()
①是否存在t,使得四边形AEFD为菱形?若存在,求出t的值;若不存在,请说明理由
②连接DE,当△DEF是直角三角形时,求t的值
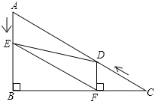
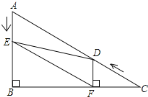
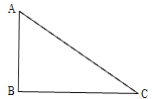

图1 图2 备用图 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=﹣2.
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究: 探究一:如图1,设△PAD的面积为S,令W=tS,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;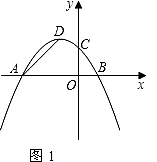
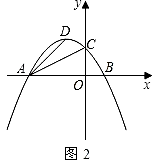
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.(参考资料:抛物线y=ax2+bx+c(a≠0)对称轴是直线x= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,空圆柱形容器内放着一个实心的“柱锥体”(由一个圆柱和一个同底面的圆锥组成的几何体).现向这个容器内匀速注水,水流速度为5cm3/s,注满为止.已知整个注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请你根据图中信息,解答下列问题: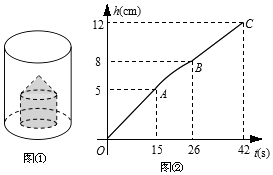
(1)圆柱形容器的高为cm,“柱锥体”中圆锥体的高为cm;
(2)分别求出圆柱形容器的底面积与“柱锥体”的底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:请根据图中给出的信息,解答下列问题:
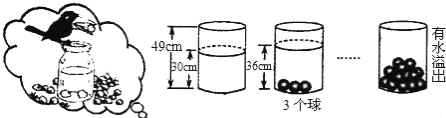
(1)放入一个小球量桶中水面升高 cm;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的函数关系式;
(3)当量桶中水面上升至距离量桶顶部3cm时,应在量桶中放入几个小球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com