练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知y＋6与x－1成正比例，且当x＝3时，y＝－10.

    (1)求y与x的函数关系式；

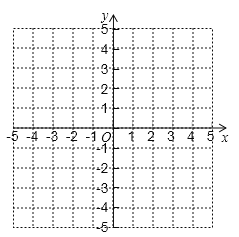
    (2)画出函数的图象．

    【答案】(1) y＝－2x－4 (2)见解析

    【解析】(1)根据正比例的定义设y＋6=k(x－1)(k≠0),然后把已知数据x＝3，y＝－10代入进行计算求出k值,即可得解;

    (2)求出与坐标轴的交点,然后利用两点法作出函数图象即可.

    (1)∵y＋6与x－1成正比例，

    ∴设y＋6＝k(x－1)(k≠0)．

    ∵当x＝3时，y＝－10，

    ∴－10＋6＝k(3－1)．解得k＝－2.

    ∴y＋6＝－2(x－1)．

    ∴函数关系式为y＝－2x－4.

    (2)当x＝0时，y＝－4；

    当y＝0时，－2x－4＝0，解得x＝－2.

    ∴函数图象经过点(0，－4)，(－2，0)．函数图象如图．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明受《乌鸦喝水》故事的启发，利用量桶和体积相同的小球进行了如下操作：请根据图中给出的信息，解答下列问题：

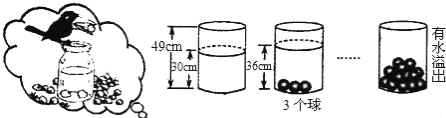
    (1)放入一个小球量桶中水面升高　 　cm；

    (2)求放入小球后量桶中水面的高度y（cm）与小球个数x（个）之间的函数关系式；

    (3)当量桶中水面上升至距离量桶顶部3cm时，应在量桶中放入几个小球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地电话拨号上网有两种收费方式，用户可以任选其一：

    （A）计时制，0.08元/分；

    （B）包月制，50元/月（限一部个人住宅电话上网）；

    此外，每种上网方式都附加通信费0.02元/分．

    （1）某用户某月上网时间为x分钟，则该用户在A、B两种收费方式下应支付费用各多少元？

    （2）如果一个月内上网200分钟和300分钟，按两种收费方式各需交费多少元？

    （3）是否存在某一时间，会出现两种收费方式一样的情况？如果存在，请求出这时的上网时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB＝AC，AD是△ABC的一条角平分线，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E.

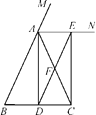
    (1)求证：四边形ADCE为矩形；

    (2)连接DE，交AC于点F，请判断四边形ABDE的形状，并证明；

    (3)线段DF与AB有怎样的关系？请直接写出你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知反比例函数y=﹣ 的图象与直线y=kx（k＜0）相交于点A、B，以AB为底作等腰三角形，使∠ACB=120°，且点C的位置随着k的不同取值而发生变化，但点C始终在某一函数图象上，则这个图象所对应的函数解析式为 ．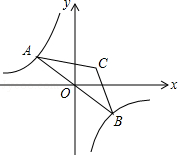

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周末，小芳骑自行车从家出发到野外郊游．从家出发0.5小时到达甲地，游玩一段时间后按原速前往乙地．小芳离家1小时20分钟后，妈妈驾车沿相同路线前往乙地，行驶10分钟时，恰好经过甲地．如图是她们距乙地的路程y（km）与小芳离家x（h）的函数图象．

    （1）小芳骑车的速度为 km/h，点H的坐标为 ．

    （2）小芳从家出发多少小时后被妈妈追上？此时距家的的路程多远？

    （3）相遇后，妈妈载上小芳和自行车同时到达乙地（彼此交流时间忽略不计），求小芳比预计时间早几分钟到达乙地？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点(点M不与B、C重合)，过点C作CN垂直DM交AB于点N，连结OM、ON、MN.下列五个结论：①△CNB≌△DMC；②；③ON⊥OM；④若AB＝2，则的最小值是1；⑤.其中正确结论是_________.(只填番号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以直线AB上一点O为端点作射线OC，将一块直角三角板的直角顶点放在O处(注：∠DOE＝90°).

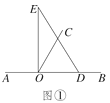
    (1)如图①，若直角三角板DOE的一边OD放在射线OB上，且∠BOC＝60°，求∠COE的度数；

    (2)如图②，将三板DOE绕O逆时针转动到某个位置时，若恰好满足5∠COD＝∠AOE，且∠BOC＝60°，求∠BOD的度数；

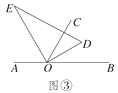
    (3)如图③，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OE恰好平分∠AOC，请说明OD所在射线是∠BOC的平分线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2﹣bx+2（a≠0）图象的顶点在第二象限，且过点（1，0），则a的取值范围是；若a+b的值为非零整数，则b的值为 ．

    查看答案和解析>>

    同步练习册答案