
【题目】已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
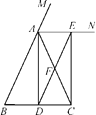
(1)求证:四边形ADCE为矩形;
(2)连接DE,交AC于点F,请判断四边形ABDE的形状,并证明;
(3)线段DF与AB有怎样的关系?请直接写出你的结论.
【答案】(1)见解析 (2) 平行四边形 (3)DF∥AB,DF=![]() AB
AB
【解析】
(1)根据三线合一可得∠ADC=90°,由外角的性质和角平分线的定义得AN∥BC,从而∠DAE=90°,由CE⊥AN得∠AEC=90°,从而四边形ADCE为矩形.
(2)由四边形ADCE为矩形,则AE=CD,AC=DE,结合已知可得AB=DE,AE=BD,从而四边形ABDE是平行四边形;
(3)由四边形ADCE为矩形可得F是AC中点,由四边形ABDE是平行四边形可得DF∥AB,从而DF是△ABC的中位线.
(1)证明:∵在△ABC中,AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,∠BAD=∠CAD.
∴∠ADC=90°.
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN.
∵AB=AC,
∴∠ABC=∠ACB,
∵∠MAN+∠CAN=∠ABC+∠ACB,
∴∠MAN=∠ABC,
∴AN∥BC,
∴∠DAE=90°.
∵CE⊥AN,
∴∠AEC=90°.
∴四边形ADCE为矩形.
(2)四边形ABDE是平行四边形.
证明:由(1)知,四边形ADCE为矩形,则AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形.
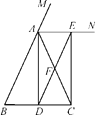
(3) ∵四边形ADCE为矩形
∴F是AC中点,
∵四边形ABDE是平行四边形
∴DF∥AB,
∴DF是△ABC的中位线.
∴DF∥AB,DF=![]() AB.
AB.


科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( ) 
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=![]() ,则四边形PEBF的周长为( )
,则四边形PEBF的周长为( )
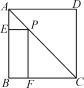
A. ![]() B. 2
B. 2![]() C. 2 D. 1
C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
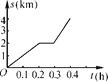
时间t/h | 0 | 0.2 | 0.3 | 0.4 |
路程s/km |
(3)路程s可以看成时间t的函数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( )
(x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( ) 
A.4.5
B.4.2
C.4
D.3.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com