
����Ŀ����ĩ��С�������г��Ӽҳ�����Ұ�⽼�Σ��Ӽҳ���0.5Сʱ����أ�����һ��ʱ���ԭ��ǰ���ҵأ�С�����1Сʱ20���Ӻ�����ݳ�����ͬ·��ǰ���ҵأ���ʻ10����ʱ��ǡ�þ����أ���ͼ�����Ǿ��ҵص�·��y��km����С�����x��h���ĺ���ͼ��
��1��С���ﳵ���ٶ�Ϊ km/h����H������Ϊ ��
��2��С���Ӽҳ�������Сʱ�������ϣ���ʱ��ҵĵ�·�̶�Զ��

��3����������������С�������г�ͬʱ�����ҵأ��˴˽���ʱ����Բ��ƣ�����С����Ԥ��ʱ���缸���ӵ����ҵأ�
���𰸡�(1) 20��H(![]() ��20)��2��25km��3��10����
��20)��2��25km��3��10����
����������1���ɺ���ͼ���Եó���С���Ҿ���ص�·��Ϊ10km������ʱ��Ϊ0.5h����С���ﳵ���ٶ�Ϊ��10��0.5=20��km/h����������ɵó�����H��������Ϊ20��������Ϊ��![]() =
=![]() ���ʵ�H������Ϊ��
���ʵ�H������Ϊ��![]() ��20����
��20����
��2����ֱ��AB�Ľ���ʽΪ��y1=k1x+b1������A��0��30����B��0.5��20������ã�y1=��20x+30����AB��CD������ֱ��CD�Ľ���ʽΪ��y2=��20x+b2������C��1��20������ã�b2=40����y2=��20x+40����ֱ��EF�Ľ���ʽΪ��y3=k3x+b3������E��![]() ��30����H��
��30����H��![]() ��20������ã�k3=��60��b3=110����y3=��60x+110���ⷽ����
��20������ã�k3=��60��b3=110����y3=��60x+110���ⷽ����![]() ����
����![]() �����D����Ϊ��1.75��5����30��5=25��km��������С������1.75Сʱ�������ϣ���ʱ���25km��
�����D����Ϊ��1.75��5����30��5=25��km��������С������1.75Сʱ�������ϣ���ʱ���25km��
��3����y=0����ֱ��CD����ʽ�У���20x+40=0�����x=2����y=0����ֱ��EF�Ľ���ʽ�У���60x+110=0�����x=![]() ��2��
��2��![]() =
=![]() ��h��=10�����ӣ�����С����Ԥ��ʱ����10���ӵ����ҵأ�
��h��=10�����ӣ�����С����Ԥ��ʱ����10���ӵ����ҵأ�



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊ�����������ֳ��С���ijУ�������ԡ������佭��Ϊ�����ͼƬ������������ί���200��ͬѧ�IJ�����Ʒ��ַ����������ߵijɼ�x������50��x<100����������Ƶ���ֲ�ֱ��ͼ����ͼ��

����������Ϣ������������⣺
(1)�벹ȫƵ���ֲ�ֱ��ͼ��
(2)�����ݳɼ�����ȡ�ֲ�����ķ������Ӳ���ͬѧ�г�40�˲μ�ͼƬ���������ܽ�������ӳɼ�80��x<90��ѡ����Ӧ������ˣ�
(3)��������һ���������Ƚ�����ֻ��25%�IJ���ͬѧ���õ�һ�Ƚ�����һ�Ƚ��ķ������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ��ֽƬ��O��ֱ��Ϊ2�����������������ഹֱ��ֱ���۵����õ��IJ�����Σ������ϵ�һ�㡰�š����������ġ���һ����Բ�������Բ�ĸ��ǣ� �� 
A.![]()
B.![]()
C.![]()
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������г�ȥѧУ�������ijһ�ٶ�������ʻ����;���г��������ϣ�ͣ�����������˼����ӣ�Ϊ�˰�ʱ��У�����ӿ����ٶȣ��Ա���������ʻ�����ʱ��У����У��С���������г��н�·��s(km)���н�ʱ��t(h)��ͼ����ͼ��ʾ����ش�
(1)���ͼ��ӳ������������֮��Ĺ�ϵ��
(2)����ͼ�������
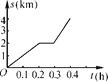
ʱ��t/h | 0 | 0.2 | 0.3 | 0.4 |
·��s/km |
(3)·��s���Կ���ʱ��t�ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪y��6��x��1�����������ҵ�x��3ʱ��y����10.
(1)��y��x�ĺ�����ϵʽ��
(2)����������ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�Ǿ���ABCD�ı�AD�ϵ�һ�����㣬���ε������߳�AB��BC�ֱ�Ϊ6��8,�Խ���AC��BD�ཻ�ڵ�O.���P�����ε������Խ���AC��BD�ľ���֮��Ϊ_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڷ���������y= ![]() ��x��0����ͼ�����е�P1��P2��P3��P4 �� P5 �� ���ǵĺ���������Ϊ2��4��6��8��10���ֱ����Щ����x����y��Ĵ��ߣ�ͼ�������ɵ���Ӱ���ֵ��������������ΪS1 �� S2 �� S3 �� S4 �� ��S1+S2+S3+S4��ֵΪ�� ��
��x��0����ͼ�����е�P1��P2��P3��P4 �� P5 �� ���ǵĺ���������Ϊ2��4��6��8��10���ֱ����Щ����x����y��Ĵ��ߣ�ͼ�������ɵ���Ӱ���ֵ��������������ΪS1 �� S2 �� S3 �� S4 �� ��S1+S2+S3+S4��ֵΪ�� �� 
A.4.5
B.4.2
C.4
D.3.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�������˶��İ����ߣ������ֻ�������¼��ij���£�30�죩ÿ�콡���ߵIJ�������λ������������¼������Ƴ�����ͼ��ʾ��ͳ��ͼ������������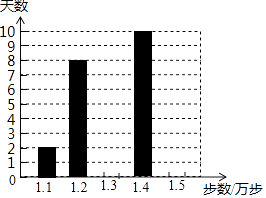
��1�������������ƽ��ÿ�콡���ߵIJ���Ϊ1.32����������1.3��1.5��������
��2�������������е���������λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��AB��һ��OΪ�˵�������OC��ʹ��BOC=70������һ��ֱ�������ε�ֱ�Ƕ�����ڵ�O������ע����DOE=90�㣩
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB�ϣ����COE=�� ���㣻
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�O��ʱ�뷽��ת����ij��λ�ã���OCǡ��ƽ�֡�BOE�����COD�Ķ�����
��3����ͼ�ۣ���ֱ�����ǰ�DOE�Ƶ�Oת�������ODʼ���ڡ�BOC���ڲ����Բ����BOD�͡�COE��������������ϵ����˵�����ɣ�
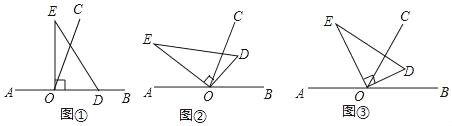
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com