
【题目】如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边长AB、BC分别为6和8,对角线AC、BD相交于点O.则点P到矩形的两条对角线AC和BD的距离之和为_____.

科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校以“我最想去的社会实践地”为课题,开展了一次调查,从全校同学中随机抽取了部分同学进行调查,每位同学从“荪湖花海”、“保国寺”、“慈城古镇”、“绿色学校”中选取一项最想去的社会实践地,并将调查结果绘制成如下的统计图(部分信息未给出).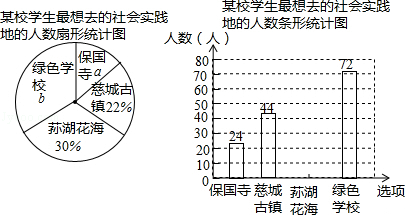
请根据统计图中信息,解答下列问题:
(1)该调查的样本容量为 , a=%,b=%,“荪湖花海”所对应扇形的圆心角度数为度.
(2)补全条形统计图;
(3)若该校共有1600名学生,请估计全校最想去“绿色学校”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小芳骑自行车从家出发到野外郊游.从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地.小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地.如图是她们距乙地的路程y(km)与小芳离家x(h)的函数图象.
(1)小芳骑车的速度为 km/h,点H的坐标为 .
(2)小芳从家出发多少小时后被妈妈追上?此时距家的的路程多远?

(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分钟到达乙地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜宾市开展“创建全国文明城市”活动,城区某校倡议学生利用双休日在“市政广场”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,绘制了不完整的统计图,根据以下图中信息,回答下列问题:

(1)将条形统计图补充完整;
(2)填空:被调查学生劳动时间的众数是______;中位数是________;
(3)求所有被调查同学的平均劳动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
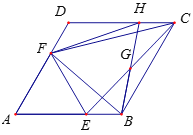
【题目】如图,在菱形ABCD中,![]() .点E、F分别是边AB、AD上的点,且满足
.点E、F分别是边AB、AD上的点,且满足![]() ,连结EF.
,连结EF.
(1)求证: ![]() 为等腰三角形;
为等腰三角形;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)若G是CE的中点,连结BG并延长交DC于点H,连结FH,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过30立方米时,按2元/立方米计费;月用水量超过30立方米时,其中的30立方米仍按2元/立方米收费,超过部分按2.5元/立方米计费.设每户家庭月用水量为x立方米.
(1)当x不超过30时,应收多少水费(用x的代数式表示);当x超过30时,应收多少水费(用x的代数式表示);
(2)小明家四月份用水20立方米,五月份用水36立方米,请帮小明计算一下他家这两个月一共应交多少元水费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在青山区“海绵城市”工程中,某工程队接受一段道路施工的任务,计划从2016年10月初至2017年9月底(12个月)完成.施工3个月后,实行倒计时,提高工作效率,剩余工程量与施工时间的关系如图所示,那么按提高工作效率后的速度做完全部工程,则工期可缩短________个月.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com