练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】乐乐是一名健步运动的爱好者，她用手机软件记录了某个月（30天）每天健步走的步数（单位：万步），并将记录结果绘制成了如图所示的统计图（不完整）．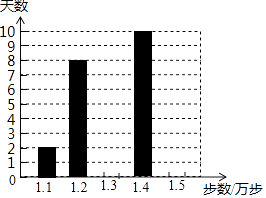

    （1）若乐乐这个月平均每天健步走的步数为1.32万步，试求她走1.3万步和1.5万步的天数；
    （2）求这组数据中的众数和中位数．

    【答案】
    （1）

    解：设她走1.3万步的天数为x天，她走1.5万步的天数为y天，

    根据题意，得： ，

    解得： ，

    ∴她走1.3万步的天数为6天，她走1.5万步的天数为4天


    （2）

    解：由条形图可知，1.4万步的天数最多，有10天，则众数为1.4万步；

    中位数为第15、16个数据的平均数，则中位数为1.3万步


    【解析】（1）她走1.3万步的天数为x天，她走1.5万步的天数为y天，根据总天数为30天且平均数为1.32万步，据此可得答案；（2）根据众数和中位数的定义解答即可得．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为(　　)

    A. 2B. C. 4D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周末，小芳骑自行车从家出发到野外郊游．从家出发0.5小时到达甲地，游玩一段时间后按原速前往乙地．小芳离家1小时20分钟后，妈妈驾车沿相同路线前往乙地，行驶10分钟时，恰好经过甲地．如图是她们距乙地的路程y（km）与小芳离家x（h）的函数图象．

    （1）小芳骑车的速度为 km/h，点H的坐标为 ．

    （2）小芳从家出发多少小时后被妈妈追上？此时距家的的路程多远？

    （3）相遇后，妈妈载上小芳和自行车同时到达乙地（彼此交流时间忽略不计），求小芳比预计时间早几分钟到达乙地？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

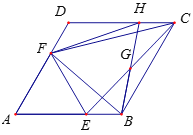
    【题目】如图，在菱形ABCD中，．点E、F分别是边AB、AD上的点，且满足，连结EF．

    （1）求证: 为等腰三角形；

    （2）若，求的面积；

    （3）若G是CE的中点，连结BG并延长交DC于点H，连结FH，求证：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以直线AB上一点O为端点作射线OC，将一块直角三角板的直角顶点放在O处(注：∠DOE＝90°).

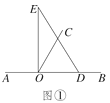
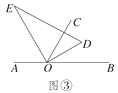
    (1)如图①，若直角三角板DOE的一边OD放在射线OB上，且∠BOC＝60°，求∠COE的度数；

    (2)如图②，将三板DOE绕O逆时针转动到某个位置时，若恰好满足5∠COD＝∠AOE，且∠BOC＝60°，求∠BOD的度数；

    (3)如图③，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OE恰好平分∠AOC，请说明OD所在射线是∠BOC的平分线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过30立方米时，按2元/立方米计费；月用水量超过30立方米时，其中的30立方米仍按2元/立方米收费，超过部分按2.5元/立方米计费．设每户家庭月用水量为x立方米．

    （1）当x不超过30时，应收多少水费（用x的代数式表示）；当x超过30时，应收多少水费（用x的代数式表示）；

    （2）小明家四月份用水20立方米，五月份用水36立方米，请帮小明计算一下他家这两个月一共应交多少元水费？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ABC=45°，AD⊥BC于点D，点E在AD上，且DE=DC．
    （1）求证：△BDE≌△ADC；
    （2）若BC=8.4，tanC= ，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A，B分别为数轴上的两点，点A表示的数是﹣30，点B表示的数是50．

    （1）请写出线段AB中点M表示的数是　 　．

    （2）现有一只蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左移动，同时另一只蚂蚁Q恰好从点A出发，以每秒2个单位长度的速度沿数轴向右移动，设两只蚂蚁在数轴上的点C相遇．

    ①求A、B两点间的距离；

    ②求两只蚂蚁在数轴上的点C相遇时所用的时间；

    ③求点C对应的数是多少？

    （3）若蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左运动，同时另一只蚂蚁恰好从A点出发，以每秒2个单位长度的速度沿数轴也向左运动，设两只蚂蚁在数轴上的D点相遇，求D点表示的数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（原题）已知直线AB∥CD，点P为平行线AB，CD之间的一点．如图1，若∠ABP=50°，∠CDP=60°，BE平分∠ABP，DE平分∠CDP，求∠BED的度数．

    （探究）如图2，当点P在直线AB的上方时，若∠ABP=α，∠CDP=β，∠ABP和∠CDP的平分线交于点E1，∠ABE1与∠CDE1的角平分线交于点E2，∠ABE2与∠CDE2的角平分线交于点E3，…以此类推，求∠En的度数．

    （变式）如图3，∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，试猜想∠P与∠E的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案