
����Ŀ����ͼ����֪A��B�ֱ�Ϊ�����ϵ����㣬��A��ʾ�����ǩ�30����B��ʾ������50��
![]()
��1����д���߶�AB�е�M��ʾ�������� ����
��2������һֻ����P�ӵ�B��������ÿ��3����λ���ȵ��ٶ������������ƶ���ͬʱ��һֻ����Qǡ�ôӵ�A��������ÿ��2����λ���ȵ��ٶ������������ƶ�������ֻ�����������ϵĵ�C������
����A��B�����ľ��룻
������ֻ�����������ϵĵ�C����ʱ���õ�ʱ�䣻
�����C��Ӧ�����Ƕ��٣�
��3��������P�ӵ�B��������ÿ��3����λ���ȵ��ٶ������������˶���ͬʱ��һֻ����ǡ�ô�A���������ÿ��2����λ���ȵ��ٶ�������Ҳ�����˶�������ֻ�����������ϵ�D����������D���ʾ�����Ƕ��٣�
���𰸡���1��10����2����80����16�룻��2����3��-190.
��������
���ȼ����AB���ȣ��ٸ����е�ƽ���߶οɵõ�M��ʾ������
��A��B��ľ����������ʾ�������мӼ����㼴�ɵã�
����·�̳����ٶȼ��ɱ�ʾʱ�䣻
����50��ȥ����P������·�̼��ɵã�
��3������ֻ����t���������������ã�����A��������������ݵ�����ϵ�г����̣�Ȼ��ɼ�����˶�ʱ�䣬�ٸ���A���ʾ�����������ɵ�D���Ӧ����.
�⣺��1��AB=50+����30��=20
��AB�е�M��ʾ������10��
�ʴ�Ϊ��10
��2����A��B�����ľ���Ϊ��50������30��=80
����ֻ�����������ϵĵ�C����ʱ���õ�ʱ��Ϊ��80�£�3+2��=16���룩
�۵�C��Ӧ�����ǣ�50��16��3=2
��3������ֻ����t����������ɵ�: 2t+80=3t
��� t=80
�� D���ʾ�����ǣ�-( ![]() )-30=��190.
)-30=��190.


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������г�ȥѧУ�������ijһ�ٶ�������ʻ����;���г��������ϣ�ͣ�����������˼����ӣ�Ϊ�˰�ʱ��У�����ӿ����ٶȣ��Ա���������ʻ�����ʱ��У����У��С���������г��н�·��s(km)���н�ʱ��t(h)��ͼ����ͼ��ʾ����ش�
(1)���ͼ��ӳ������������֮��Ĺ�ϵ��
(2)����ͼ�������
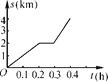
ʱ��t/h | 0 | 0.2 | 0.3 | 0.4 |
·��s/km |
(3)·��s���Կ���ʱ��t�ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�������˶��İ����ߣ������ֻ�������¼��ij���£�30�죩ÿ�콡���ߵIJ�������λ������������¼������Ƴ�����ͼ��ʾ��ͳ��ͼ������������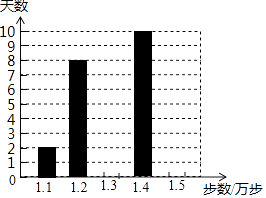
��1�������������ƽ��ÿ�콡���ߵIJ���Ϊ1.32����������1.3��1.5��������
��2�������������е���������λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1����ͼ�٣��ı���ABCD�������Σ���G��BC�ϵ�����һ�㣬BF��AG�ڵ�F��DE��AG�ڵ�E��̽��BF��DE��EF֮���������ϵ����һѧϰС�����̽���õ�DE��BF=EF����֤��������ۣ� 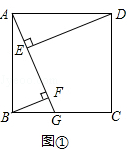
��2������1���еĵ�G��CB���ӳ����ϣ������������䣬����ͼ���л���ͼ�Σ���ֱ��д����ʱBF��DE��EF֮���������ϵ�� 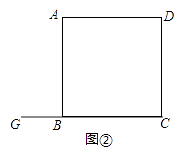
��3����ͼ�ۣ��ı���ABCD�ڽ��ڡ�O��AB=AD��E��F��AC�ϵ����㣬�������AED=��BFA=��BCD�����ж�AC��DE��BF֮���������ϵ����˵�����ɣ� 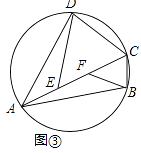
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��F�ֱ���OA��OC��
��1������������������OB=OD���ڡ�1=��2����OE=OF���������ѡȡ��������֤����BEO�ա�DFO��
��2���ڣ�1������������ѡ������ǰ���£�����AE=CF����֤���ı���ABCD��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������ڵĽ������ڽ��ŵؽ��У����д�����ɳʯ��Ҫ���䣮���氲��������������Ϊ8�֡�10�ֵĿ�����12����ȫ����������һ��������110��ɳʯ��
��1�������氲������������Ϊ8�֡�10�ֵĿ������ж�������
��2�����Ź��̵Ľ�չ�����氲��������Ҫһ������ɳʯ165�����ϣ�Ϊ����������������������ֿ�����6���������ж����ֹ���������һһд����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
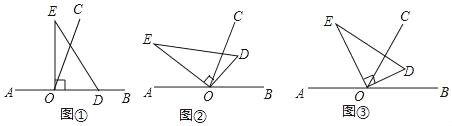
����Ŀ����ͼ����ֱ��AB��һ��OΪ�˵�������OC��ʹ��BOC=70������һ��ֱ�������ε�ֱ�Ƕ�����ڵ�O������ע����DOE=90�㣩
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB�ϣ����COE=�� ���㣻
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�O��ʱ�뷽��ת����ij��λ�ã���OCǡ��ƽ�֡�BOE�����COD�Ķ�����
��3����ͼ�ۣ���ֱ�����ǰ�DOE�Ƶ�Oת�������ODʼ���ڡ�BOC���ڲ����Բ����BOD�͡�COE��������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������乲120�ˣ����м׳����������ҳ���������4����5��.
��1����ס�����������ж����ˣ�
��2�����Ӽס���������ֱ������ˣ���ɱ����������²�Ʒ����ʹ�ס��ҡ������������������Ϊ13��4��7����ô�ס���������Ҫ�ֱ������ٹ��ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������н�����ͼ��ֱ������ϵ����������A��O��B��λ����ͼ�����Ƿֱ���(��1��1)��(0��0)��(1��0)��
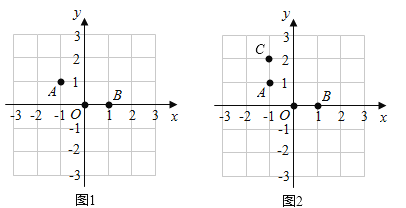
(1)��ͼ2����������C��ʹA��O��B��C�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ�����ͼ�л�����ͼ�εĶԳ��
(2)���������λ������һ������P��ʹA��O��B��P�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ���ֱ��д������P��λ�õ����꣮(д��2������)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com