
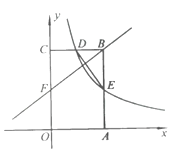
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)直接写出k的值及点E的坐标;
(2)若点F是OC边上一点,且FB⊥DE,求直线FB的解析式.
【答案】(1)k=3,(2,![]() )(2)y=
)(2)y=![]()
【解析】
分析: (1)先根据点B的坐标为(2,3)求出D点坐标,代入反比例函数解析式即可求出k的值,进而得出解析式,再把x=2代入求出y的值即可得出E点坐标,
(2)根据FB⊥DE,利用同角的余角相等得到一组等角,再根据两直角相等进而得出△FBC∽△DEB,根据相似三角形的性质进而求出F点的坐标,利用待定系数法求出直线FB的解析式即可.
详解:(1)∵点B的坐标为(2,3),点D是BC的中点,
∴D(1,3),
∵点D在反比例函数![]() (x>0)上,
(x>0)上,
∴3=![]() ,解得k=3,
,解得k=3,
∴反比例函数的解析式为:![]() .
.
∵四边形OABC是矩形,点B的坐标为(2,3),
∴当x=2时,y=![]() ,
,
∴E点坐标为(2,![]() )
)
(2)因为FB⊥DE,
∴∠CBF+∠EDB=90°,∠BED+∠EDB=90°,
∴∠CBF=∠BDE,
因为∠C=∠DBE=90°,
∴△FBC∽△DEB,
∵点E的坐标为(2,![]() ),B的坐标为(2,3),点D的坐标为(1,3),
),B的坐标为(2,3),点D的坐标为(1,3),
∴BD=1,BE=![]() ,BC=2,
,BC=2,
∵△FBC∽△DEB,
∴![]() ,
,
即:![]() ,
,
∴FC=![]() ,
,
∴点F的坐标为(0,![]() ),
),
设直线FB的解析式y=kx+b,
则2k+b=3,b=![]() ,
,
解得:k=![]() ,
,
∴直线FB的解析式y=![]() .
.
点睛:本题主考查反比例函数与几何综合,解决本题的关键是要熟练掌握反比例函数图象上点的坐标特征,要求学生利用相似三角形的性质进行综合分析.


科目:初中数学 来源: 题型:
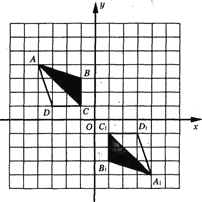
【题目】如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD 绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.
(1)直接写出点D1的坐标________,点D旋转到点D1所经过的路线长_______;
(2)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是________,则它所对应的正弦函数值是_________;
(3)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2(4,5),画出平移后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距160km,![]() 、
、![]() 两车分别从甲、乙两地同时出发,
两车分别从甲、乙两地同时出发,![]() 车速度为85km/h,
车速度为85km/h,![]() 车速度为65km/h.
车速度为65km/h.
(1)![]() 、
、![]() 两车同时同向而行,
两车同时同向而行,![]() 车在后,经过几小时
车在后,经过几小时![]() 车追上
车追上![]() 车?
车?
(2)![]() 、
、![]() 两车同时相向而行,经过几小时两车相距20km?
两车同时相向而行,经过几小时两车相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
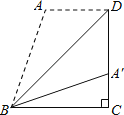
【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=20°,则∠A′BD的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数![]() .(利润=售价-制造成本)
.(利润=售价-制造成本)
(1)写出每月的利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?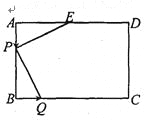
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线上![]() ,它与
,它与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() ,
,![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,
之间的一点,
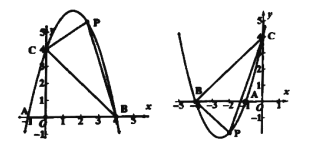
(1)当![]() 时,求抛物线的方程,并求出当
时,求抛物线的方程,并求出当![]() 面积最大时的
面积最大时的![]() 的横坐标。
的横坐标。
(2)当![]() 时,求抛物线的方程及
时,求抛物线的方程及![]() 的坐标,并求当
的坐标,并求当![]() 面积最大时
面积最大时![]() 的横坐标。
的横坐标。
(3)根据(1)、(2)推断![]() 的横坐标与
的横坐标与![]() 的横坐标有何关系?
的横坐标有何关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
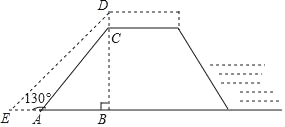
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com