
 如图,在平面直角坐标系xOy中,一次函数y=x与二次函数y=x2+bx的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
如图,在平面直角坐标系xOy中,一次函数y=x与二次函数y=x2+bx的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.分析 (1)把点A(3,3)代入y=x2+bx中,即可解决问题.
(2)设点P在点Q的左下方,过点P作PE⊥QQ1于点E,如图1所示.设点P(m,m)(0<m<1),则Q(m+2,m+2),P1(m,m2-2m),Q1(m+2,m2+2m),构建二次函数,利用二次函数性质即可解决问题.
(3)存在,首先证明EF是线段AM的中垂线,利用方程组求交点E坐标,再根据对称性E关于点A的对称点E′也符合条件,求出E、E′坐标即可.
解答 解:(1)把点A(3,3)代入y=x2+bx中,
得:3=9+3b,解得:b=-2,
∴二次函数的表达式为y=x2-2x.
(2)设点P在点Q的左下方,过点P作PE⊥QQ1于点E,如图1所示.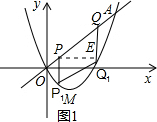
∵PE⊥QQ1,QQ1⊥x轴,
∴PE∥x轴,
∵直线OA的解析式为y=x,
∴∠QPE=45°,
∴PE=$\frac{\sqrt{2}}{2}$PQ=2.
设点P(m,m)(0<m<1),则Q(m+2,m+2),P1(m,m2-2m),Q1(m+2,m2+2m),
∴PP1=3m-m2,QQ1=2-m2-m,
∴${S}_{梯形PQ{Q}_{1}{P}_{1}}$=$\frac{1}{2}$(PP1+QQ1)•PE=-2m2+2m+2=-2$(m-\frac{1}{2})^{2}$+$\frac{5}{2}$,
∴当m=$\frac{1}{2}$时,${S}_{梯形PQ{Q}_{1}{P}_{1}}$取最大值,最大值为$\frac{5}{2}$.
(3)存在.
如图2中,①点E的对称点为F,EF与AM交于点G,连接OM、MF、AF、OF.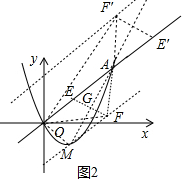
∵S△AOF=S△AOM,
∴MF∥OA,
∵EG=GF,$\frac{EG}{FG}$=$\frac{AG}{GM}$,
∴AG=GM,
∵M(1,-1),A(3,3),
∴点G(2,1),
∵直线AM解析式为y=2x-3,
∴线段AM的中垂线EF的解析式为y=-$\frac{1}{2}$x+2,
由$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{2}x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{4}{3}}\end{array}\right.$,
∴点E坐标为($\frac{4}{3}$,$\frac{4}{3}$).
②设E关于点A的对称点E′,E′关于AM的对称点F′,根据对称性可知,△OAF′与△AOF的面积相等,
此时E′($\frac{14}{3}$,$\frac{14}{3}$),
综上所述满足条件的点E坐标($\frac{4}{3}$,$\frac{4}{3}$)或($\frac{14}{3}$,$\frac{14}{3}$).
点评 本题考查二次函数综合题、待定系数法、平行线的性质、一次函数、面积问题等知识,解题的关键是灵活应用待定系数法确定函数解析式,学会构建二次函数,利用二次函数性质解决最值问题,学会利用方程组求两个函数的交点,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
 直角三角形ABC,∠C=90°,四边形CDEF是正方形,其中点D、E、F分别在边AC、AB、BC上,如果AE=a,EB=b,则三角形ADE与三角形EFB的面积之和是$\frac{ab}{2}$.
直角三角形ABC,∠C=90°,四边形CDEF是正方形,其中点D、E、F分别在边AC、AB、BC上,如果AE=a,EB=b,则三角形ADE与三角形EFB的面积之和是$\frac{ab}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=mx2-4mx-12m(m>0)与x轴交于A、B两点,与y轴交于点C,点E为BC的中点,点D为抛物线的顶点,且OC=OB.
如图,抛物线y=mx2-4mx-12m(m>0)与x轴交于A、B两点,与y轴交于点C,点E为BC的中点,点D为抛物线的顶点,且OC=OB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
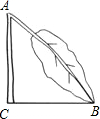 一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号)
一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 搭一搭,算一算;
搭一搭,算一算;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com