
ЁОЬтФПЁПШчЭМ1ЃЌШєЫФБпаЮABCDЁЂGFEDЖМЪЧе§ЗНаЮЃЌЯдШЛЭМжагаAGЃНCEЃЌAGЁЭCEЃЎ
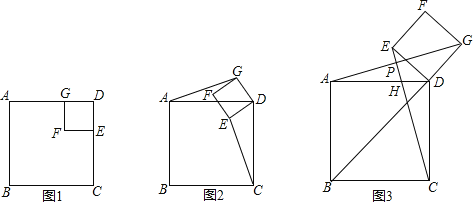
ЃЈ1ЃЉЕБе§ЗНаЮGFEDШЦDа§зЊЕНШчЭМ2ЕФЮЛжУЪБЃЌAGЃНCEЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыИјГіжЄУїЃЌШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЕБе§ЗНаЮGFEDШЦDа§зЊЕНBЃЌDЃЌGдквЛЬѕжБЯпЃЈШчЭМ3ЃЉЩЯЪБЃЌСЌНсCEЃЌЩшCEЗжБ№НЛAGЁЂADгкPЁЂHЃЎ
ЂйЧѓжЄЃКAGЁЭCEЃЛ
ЂкШчЙћЃЌADЃН2![]() ЃЌDGЃН
ЃЌDGЃН![]() ЃЌЧѓCEЕФГЄЃЎ
ЃЌЧѓCEЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉAGЃНCEГЩСЂЃЛЃЈ2ЃЉЂйЯъМћНтЮіЃЛЂк5![]()
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУе§ЗНаЮаджЪвдМАШЋЕШШ§НЧаЮЕФХаЖЈЕФКмДжЁїAGDЁеЁїCEDЃЈSASЃЉМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉЂйИљОнЃЈ1ЃЉЕУГіЁЯ1ЃНЁЯ2ЃЌдйРћгУЁЯ3ЃНЁЯ4ЃЌЁЯ4+ЁЯ2ЃН90ЁуЃЌПЩЕУГіЁЯ3+ЁЯ1ЃН90ЁуЃЌНјЖјЕУГіД№АИЃЛ
ЂкРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУГіMDЃНMGЃН![]() ЃЌНјЖјРћгУЙДЙЩЖЈРэЧѓГіCEЕФГЄЃЎ
ЃЌНјЖјРћгУЙДЙЩЖЈРэЧѓГіCEЕФГЄЃЎ
ЃЈ1ЃЉНтЃКAGЃНCEГЩСЂЃЎ
РэгЩЃКЁпЫФБпаЮABCDЁЂЫФБпаЮDEFGЪЧе§ЗНаЮЃЌ
ЁрGDЃНDEЃЌADЃНDCЃЌ
ЁЯGDEЃНЁЯADCЃН90ЁуЃЌ
ЁрЁЯGDAЃН90ЁуЉЁЯADEЃНЁЯEDCЃЌ
дкЁїAGDКЭЁїCEDжаЃЌ
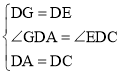
ЁрЁїAGDЁеЁїCEDЃЈSASЃЉЃЌ
ЁрAGЃНCEЃЛ
ЃЈ2ЃЉжЄУїЃКЂйгЩЃЈ1ЃЉПЩжЊЁїAGDЁеЁїCEDЃЌ
ЁрЁЯ1ЃНЁЯ2ЃЌ
ЁпЁЯ3ЃНЁЯ4ЃЌЁЯ4+ЁЯ2ЃН90ЁуЃЌ
ЁрЁЯ3+ЁЯ1ЃН90ЁуЃЌ
ЁрЁЯAPHЃН90ЁуЃЌ
ЁрAGЁЭCHЃЛ
ЂкНтЃКЙ§GзїGMЁЭADгкMЃЎ
ЁпBDЪЧе§ЗНаЮABCDЕФЖдНЧЯпЃЌ
ЁрЁЯADBЃНЁЯGDMЃН45ЁуЃЌ
ЁрЁЯDGMЃН45ЁуЃЌ
ЁпDGЃН![]() ЃЌ
ЃЌ
ЁрMDЃНMGЃН![]() ЃЌ
ЃЌ
дкRtЁїAMGжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
ЁрCEЃНAGЃН5![]() ЃЎ
ЃЎ


 КшЭМЭМЪщКЎМйзївЕМйЦкзївЕМЊСжДѓбЇГіАцЩчЯЕСаД№АИ
КшЭМЭМЪщКЎМйзївЕМйЦкзївЕМЊСжДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаОгУёЕФНЛЭЈЯћЗбПЩЗжЮЊНЛЭЈЙЄОпЁЂНЛЭЈЙЄОпЪЙгУШМСЯЁЂНЛЭЈЙЄОпЮЌаоЁЂЪаФкЙЋЙВНЛЭЈЁЂГЧЪаМфНЛЭЈЮхЯю.ИУЪаЭГМЦОжИљОнЕБФъИїЯюЕФШЈжиМАИїЯюМлИёЕФеЧЗљЃЌМЦЫуЕБФъОгУёНЛЭЈЯћЗбМлИёЕФЦНОљеЧЗљ.2017ФъИУЪаЕФгаЙиЪ§ОнШчЯТБэЫљЪО.
НЛЭЈЙЄОп | НЛЭЈЙЄОпЪЙгУШМСЯ | НЛЭЈЙЄОпЮЌао | ЪаФкЙЋЙВНЛЭЈ | ГЧЪаМфНЛЭЈ | |
еМНЛЭЈЯћЗбЕФБШР§ | 22% | 13% | 5% | P | 26% |
ЯрЖдЩЯвЛФъМлИёЕФеЧЗљ | 1.5% | m% | 2% | 0.5% | 1% |
ЃЈ1ЃЉЧѓpЕФжЕЃЛ
ЃЈ2ЃЉШє2017ФъИУЪаЕФОгУёНЛЭЈЯћЗбЯрЖдЩЯвЛФъМлИёЕФЦНОљеЧЗљЮЊ1.25%ЃЌЧѓmЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2-2(k-1)x+k2 =0гаСНИіЪЕЪ§Иљx1.x2.
(1)ЧѓЪЕ Ъ§kЕФШЁжЕЗЖЮЇ;
(2)Шє(x1+1)(x2+1)=2ЃЌЪдЧѓkЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцзјБъЯЕxOyжаЃЌЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌЕуPЕФКсзјБъЮЊ2ЃЌНЋЕуAШЦЕуPа§зЊЃЌЪЙЫќЕФЖдгІЕуBЧЁКУТфдкxжсЩЯЃЈВЛгыAЕужиКЯЃЉЃЛдйНЋЕуBШЦЕуOФцЪБеыа§зЊ90ЁуЕУЕНЕуCЃЎ
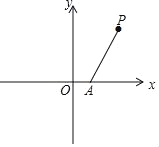
ЃЈ1ЃЉжБНгаДГіЕуBКЭЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЧѓОЙ§AЃЌBЃЌCШ§ЕуЕФХзЮяЯпЕФБэДяЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ3ЗжЃЉШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ3cmЃЌЖЏЕуPДгBЕуГіЗЂвд3cm/sЕФЫйЖШбизХБпBCЉCDЉDAдЫЖЏЃЌЕНДяAЕуЭЃжЙдЫЖЏЃЛСэвЛЖЏЕуQЭЌЪБДгBЕуГіЗЂЃЌвд1cm/sЕФЫйЖШбизХБпBAЯђAЕудЫЖЏЃЌЕНДяAЕуЭЃжЙдЫЖЏЃЎЩшPЕудЫЖЏЪБМфЮЊxЃЈsЃЉЃЌЁїBPQЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЌдђyЙигкxЕФКЏЪ§ЭМЯѓЪЧЃЈ ЃЉ
AЃЎ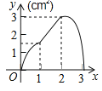 BЃЎ
BЃЎ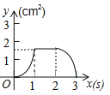 CЃЎ
CЃЎ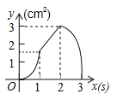 DЃЎ
DЃЎ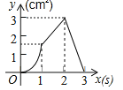
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛеХОиаЮжНЦЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЯжНЋетеХжНЦЌАДЯТСаЭМЪОЗНЗЈелЕўЃЌЧыНтОіЯТСаЮЪЬтЃК
ЃЌЯжНЋетеХжНЦЌАДЯТСаЭМЪОЗНЗЈелЕўЃЌЧыНтОіЯТСаЮЪЬтЃК
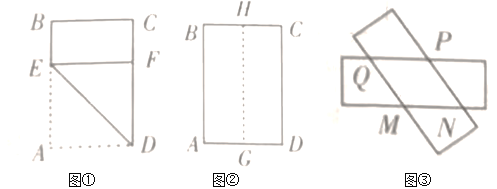
ЃЈ1ЃЉШчЭМЂйЃЌелКлЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФЖдгІЕу
ЕФЖдгІЕу![]() дк
дк![]() ЩЯЃЌЧѓжЄЃКЫФБпаЮ
ЩЯЃЌЧѓжЄЃКЫФБпаЮ![]() ЪЧе§ЗНаЮЃЛ
ЪЧе§ЗНаЮЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЌАбОиаЮжНЦЌ
ЕФжаЕуЃЌАбОиаЮжНЦЌ![]() бизХ
бизХ![]() МєПЊЃЌБфГЩСНеХОиаЮжНЦЌЃЌНЋСНеХжНЦЌШЮвтЕўКЯКѓЃЈШчЭМЂлЃЉЃЌХаЖЯжиЕўЫФБпаЮ
МєПЊЃЌБфГЩСНеХОиаЮжНЦЌЃЌНЋСНеХжНЦЌШЮвтЕўКЯКѓЃЈШчЭМЂлЃЉЃЌХаЖЯжиЕўЫФБпаЮ![]() ЕФаЮзДЃЌВЂжЄУїЃЛ
ЕФаЮзДЃЌВЂжЄУїЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉжаЃЌжиЕўЫФБпаЮ![]() ЕФжмГЄЪЧЗёДцдкзюДѓжЕЛђзюаЁжЕЃПШєДцдкЃЌЧыЧѓГізюДѓжЕЛђзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжмГЄЪЧЗёДцдкзюДѓжЕЛђзюаЁжЕЃПШєДцдкЃЌЧыЧѓГізюДѓжЕЛђзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЖўДЮКЏЪ§yЃНx2Љmx+![]() m+1(mЮЊГЃЪ§).ШєетИіЖўДЮКЏЪ§ЕФЭМЯѓгыxжсжЛгавЛИіЙЋЙВЕуAЃЌЧвAЕудкxжсЕФе§АыжсЩЯ.
m+1(mЮЊГЃЪ§).ШєетИіЖўДЮКЏЪ§ЕФЭМЯѓгыxжсжЛгавЛИіЙЋЙВЕуAЃЌЧвAЕудкxжсЕФе§АыжсЩЯ.
(1)ЧѓmЕФжЕ.
(2)ЫФБпаЮAOBCЪЧе§ЗНаЮЃЌЧвЕуBдкyжсЕФИКАыжсЩЯЃЌЯжНЋетИіЖўДЮКЏЪ§ЕФЭМЯѓЦНвЦЃЌЪЙЦНвЦКѓЕФКЏЪ§ЭМЯѓЧЁКУОЙ§BЃЌCСНЕуЃЌЧѓЦНвЦКѓЕФЭМЯѓЖдгІЕФКЏЪ§НтЮіЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
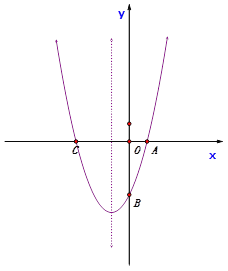
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ОЙ§ЕуAЃЈ1,0ЃЉКЭЕуB ЃЈ0ЃЌ-3ЃЉЃЌгыxжсНЛгкСэвЛЕуCЁЃ
ОЙ§ЕуAЃЈ1,0ЃЉКЭЕуB ЃЈ0ЃЌ-3ЃЉЃЌгыxжсНЛгкСэвЛЕуCЁЃ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЁЃ
ЃЈ2ЃЉдкХзЮяЯпЩЯЪЧЗёДцдквЛЕуDЃЌЪЙЁїACDЕФУцЛ§гыЁїABCЕФУцЛ§ЯрЕШЃЈЕуDВЛгыЕуBжиКЯЃЉЃПШєДцдкЃЌЧѓГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ЃЈ3ЃЉШєЕуPЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЕуQЪЧХзЮяЯпЖдГЦжсЩЯЕФЖЏЕуЃЌФЧУДЪЧЗёДцдкетбљЕФЕуPЃЌЪЙвдЕуAЁЂCЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ ABCD ЕФБпГЄЮЊ 8ЃЌE ЪЧ BC БпЕФжаЕуЃЌЕу P дкЩфЯп AD ЩЯЃЌ Й§ P зї PFЁЭAE гк FЃЎ
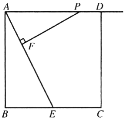
ЃЈ1ЃЉЧыХаЖЯЁїPFA гыЁїABE ЪЧЗёЯрЫЦЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЕБЕу P дкЩфЯп AD ЩЯдЫЖЏЪБЃЌЩш PAЃНxЃЌЪЧЗёДцдкЪЕЪ§ xЃЌЪЙвд PЃЌFЃЌE ЮЊЖЅ ЕуЕФШ§НЧаЮвВгыЁїABE ЯрЫЦЃПШєДцдкЃЌЧыЧѓГі x ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com