
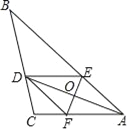
【题目】如图,在△ABC中,AD平分∠BAC,过AD的中点O作EF⊥AD,分别交AB、AC于点E、F,连接DE、DF.
(1)判断四边形AFDE是什么四边形?请说明理由;
(2)若BD=8,CD=3,AE=4,求CF的长.
【答案】(1)四边形AEDF是菱形,理由见解析;(2)CF= ![]() .
.
【解析】试题分析:(1)由于O是AD的中点,且EF⊥AD,所以AE=DE,AF=DF,由于AD平分∠BAC,所以∠EAO=∠FAO=90°,从易证AE=AF=DF=DE,所以四边形AEDF是菱形.
(2)由DE∥AC可知△BDE∽△BCA,从而可知![]() ,代入数据即可求出AC的长度,从而可知CF的长度.
,代入数据即可求出AC的长度,从而可知CF的长度.
试题解析:(1)四边形AEDF是菱形,理由如下:
∵O是AD的中点,且EF⊥AD,
∴AE=DE,AF=DF,
∵AD平分∠BAC,
∴∠EAO=∠FAO,
∵∠EOA=∠FOA=90°,
∴∠OEA=∠OFA,
∴AE=AF,
∴AE=AF=DF=DE,
∴四边形AEDF是菱形.
(2)∵四边形AEDF是菱形,
∴DE∥AC.
∴△BDE∽△BCA.
∴![]() ,
,
∴![]()
∴AC=![]()
∴CF=AC﹣CF=![]() .
.



 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=![]() x+m经过点A(﹣2,n),B(1,
x+m经过点A(﹣2,n),B(1, ![]() ),抛物线y=x2﹣2tx+t2﹣1与x轴相交于点C,D.
),抛物线y=x2﹣2tx+t2﹣1与x轴相交于点C,D.
(1)求点A的坐标;
(2)设点E的坐标为(![]() ,0),若点C,D都在线段OE上,求t的取值范围;
,0),若点C,D都在线段OE上,求t的取值范围;
(3)若该抛物线与线段AB有公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
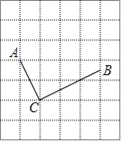
【题目】如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.
(Ⅰ)计算AB的长等于_____;
(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,“五一”小长假期间,大连市共接待海内外游客825400余人次,数825100用科学记数法表示为( )
A.8251×102
B.825.1×103
C.82.51×104
D.8.251×105
查看答案和解析>>
科目:初中数学 来源: 题型:
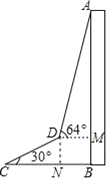
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一种边长为m厘米的正方形地砖,材料的成本价为每平方厘米n元,如果将地砖的一边扩大5厘米,另一边缩短5厘米,改成生产长方形的地砖,这种长方形地砖与正方形的地砖相比,每块的材料成本价变化情况是( )
A.没有变化
B.减少了5n元
C.增加5n元
D.减少了25n元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要设计一块面积为10平方米的正方形广告牌,公司在设计广告时,必须知道这个正方形的边长.这个正方形的边长是多少?估计边长的值(结果精确到十分位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 的纵坐标满足
的纵坐标满足![]() , 则称点
, 则称点![]() 是点
是点![]() 的“绝对点”.
的“绝对点”.
(![]() )点
)点![]() 的“绝对点”的坐标为.
的“绝对点”的坐标为.
(![]() )点
)点![]() 是函数
是函数![]() 的图像上的一点,点
的图像上的一点,点![]() 是点
是点![]() 的“绝对点”.若点
的“绝对点”.若点![]() 与点
与点![]() 重合,求点
重合,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 的“绝对点”
的“绝对点”![]() 是函数
是函数![]() 的图像上的一点.当
的图像上的一点.当![]() 时,求线段
时,求线段![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com