
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒
点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒![]() 过点D作
过点D作![]() 于点F,连接DE、EF.
于点F,连接DE、EF.
![]() 求证:
求证:![]() ;
;
![]() 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
![]() 当t为何值时,
当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.

【答案】(1)证明见解析;(2)能,理由见解析;(3)![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.
【解析】
![]() 在
在![]() 中,
中,![]() ,
,![]() ,根据30°角直角三角形的性质及已知条件即可证得结论;
,根据30°角直角三角形的性质及已知条件即可证得结论;![]() 先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;
先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;![]() 时,四边形EBFD为矩形
时,四边形EBFD为矩形![]() 在Rt△AED中求可得
在Rt△AED中求可得![]() ,由此即可解答;
,由此即可解答;![]() 时,由
时,由![]() 知
知![]() ,则得
,则得![]() ,求得
,求得![]() ,由此列方程求解即可;
,由此列方程求解即可;![]() 时,此种情况不存在.
时,此种情况不存在.
![]() 证明:在
证明:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() 解:能
解:能![]() 理由如下:
理由如下:
![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() 四边形AEFD为平行四边形.
四边形AEFD为平行四边形.
![]() ,
,
![]() .
.
![]() .
.
若使AEFD为菱形,则需![]() ,
,
即![]() ,
,![]() .
.
即当![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.
![]() 解:
解:![]() 时,四边形EBFD为矩形.
时,四边形EBFD为矩形.
在![]() 中,
中,![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,由
时,由![]() 四边形AEFD为平行四边形知
四边形AEFD为平行四边形知![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,此种情况不存在.
时,此种情况不存在.
综上所述,当![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象经过点A(6,﹣3)和点B(﹣2,5).
(1)求这个一次函数的表达式.
(2)求该函数图象与坐标轴围成的三角形的面积.
(3)判断点C(2,2)是在直线AB的上方(右边)还是下方(左边).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 P是线段 AB上的一点,![]() ,C, D两点从 A, P同时出发,分别以2
,C, D两点从 A, P同时出发,分别以2 ![]() ,1
,1![]() 的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=
的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=![]()
![]() ,点 C,D的运动时间为
,点 C,D的运动时间为![]() .
.
(1)用含![]() 和 的代数式表示线段 CP 的长度.
和 的代数式表示线段 CP 的长度.
(2)当 t =5时,![]() ,求线段 AB的长.
,求线段 AB的长.
(3)当 BC-AC=PC时,求 ![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.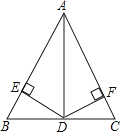
(1)求证:AB=AC;
(2)若AD=2 ![]() ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.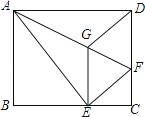
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2 ![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标为(﹣2,0),直线y=﹣ ![]() x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点.
x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点. 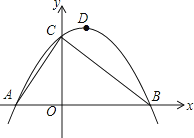
(1)请直接写出B、C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】之前我们学习了一元一次方程的解法,下面是一道解一元一次方程的题:
解方程![]() ﹣
﹣![]() =1
=1
老师说:这是一道含有分母的一元一次方程,我们可以根据等式的性质,可以把方程的两边同乘以6,这样就可以去掉分母了.于是,小明按照老师说的方法进行了解答,小明同学的解题过程如下:
解:方程两边同时乘以6,得![]() ×6﹣
×6﹣![]() ×6=1…………①
×6=1…………①
去分母,得:2(2﹣3x)﹣3(x﹣5)=1………②
去括号,得:4﹣6x﹣3x+15=1……………③
移项,得:﹣6x﹣3x=1﹣4﹣15…………④
合并同类项,得﹣9x=﹣18……………⑤
系数化1,得:x=2………………⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现从A,B两市场向甲、乙两地运送水果,A,B两个水果市场分别有水果35和15吨,其中甲地需要水果20吨,乙地需要水果30吨,从A到甲地运费50元/吨,到乙地30元/吨;从B到甲地运费60元/吨,到乙地45元/吨
(1)设A市场向甲地运送水果x吨,请完成表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A市场 | x |
|
B市场 |
|
|
(2)设总运费为W元,请写出W与x的函数关系式,写明x的取值范围;
(3)怎样调运水果才能使运费最少?运费最少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com