
°æƒø°ø»ÁÕº£¨“—÷™µ„Aµƒ◊¯±ÍŒ™£®©Å2£¨0£©£¨÷±œfly=©Å ![]() x+3”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„B∫Õµ„C£¨¡¨Ω”AC£¨∂•µ„Œ™Dµƒ≈◊ŒÔœfly=ax2+bx+cπ˝A°¢B°¢C»˝µ„£Æ
x+3”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„B∫Õµ„C£¨¡¨Ω”AC£¨∂•µ„Œ™Dµƒ≈◊ŒÔœfly=ax2+bx+cπ˝A°¢B°¢C»˝µ„£Æ 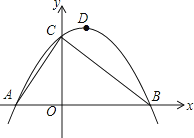
£®1£©«Î÷±Ω”–¥≥ˆB°¢C¡Ωµ„µƒ◊¯±Í£¨≈◊ŒÔœflµƒΩ‚Œˆ Ωº∞∂•µ„Dµƒ◊¯±Í£ª
£®2£©…Ë≈◊ŒÔœflµƒ∂‘≥∆÷·DEΩªœfl∂ŒBC”⁄µ„E£¨P «µ⁄“ªœÛœfiƒ⁄≈◊ŒÔœfl…œ“ªµ„£¨π˝µ„P◊˜x÷·µƒ¥πœfl£¨Ωªœfl∂ŒBC”⁄µ„F£¨»ÙÀƒ±fl–ŒDEFPŒ™∆Ω––Àƒ±fl–Œ£¨«Ûµ„Pµƒ◊¯±Í£ª
£®3£©…˵„M «œfl∂ŒBC…œµƒ“ª∂ص„£¨π˝µ„M◊˜MN°ŒAB£¨ΩªAC”⁄µ„N£¨µ„Q¥”µ„B≥ˆ∑¢£¨“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»—ÿœfl∂ŒBAœÚµ„A‘À∂Ø£¨‘À∂Ø ±º‰Œ™t£®√Σ©£¨µ±t£®√Σ©Œ™∫Œ÷µ ±£¨¥Ê‘⁄°˜QMNŒ™µ»—¸÷±Ω«»˝Ω«–Œ£ø
°æ¥∞∏°ø
£®1£©
Ω‚£∫¡Óx=0¥˙»Îy=©Å ![]() x+3
x+3
°‡y=3£¨
°‡C£®0£¨3£©£¨
¡Óy=0¥˙»Îy=©Å ![]() x+3
x+3
°‡x=4£¨
°‡B£®4£¨0£©£¨
…Ë≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™£∫y=a£®x+2£©£®x©Å4£©£¨
∞—C£®0£¨3£©¥˙»Îy=a£®x+2£©£®x©Å4£©£¨
°‡a=©Å ![]() £¨
£¨
°‡≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™£∫y=©Å ![]() £®x+2£©£®x©Å4£©=©Å
£®x+2£©£®x©Å4£©=©Å ![]() x2+
x2+ ![]() x+3£¨
x+3£¨
°‡∂•µ„Dµƒ◊¯±ÍŒ™£®1£¨ ![]() £©
£©
£®2£©
Ω‚£∫
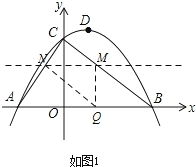
µ±DP°ŒBC ±£¨
¥À ±Àƒ±fl–ŒDEFP «∆Ω––Àƒ±fl–Œ£¨
…Ë÷±œflDPµƒΩ‚Œˆ ΩŒ™y=mx+n£¨
°fl÷±œflBCµƒΩ‚Œˆ ΩŒ™£∫y=©Å ![]() x+3£¨
x+3£¨
°‡m=©Å ![]() £¨
£¨
°‡y=©Å ![]() x+n£¨
x+n£¨
∞—D£®1£¨ ![]() £©¥˙»Îy=©Å
£©¥˙»Îy=©Å ![]() x+n£¨
x+n£¨
°‡n= ![]() £¨
£¨
°‡÷±œflDPµƒΩ‚Œˆ ΩŒ™y=©Å ![]() x+
x+ ![]() £¨
£¨
°‡¡™¡¢ 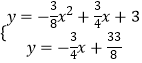 £¨
£¨
Ω‚µ√£∫x=3ªÚx=1£®…·»•£©£¨
°‡∞—x=3¥˙»Îy=©Å ![]() x+
x+ ![]() £¨
£¨
y= ![]() £¨
£¨
°‡Pµƒ◊¯±ÍŒ™£®3£¨ ![]() £©
£©
£®3£©
Ω‚£∫”…“‚ø…÷™£∫0°‹t°‹6£¨
…Ë÷±œflACµƒΩ‚Œˆ ΩŒ™£∫y=m1x+n1£¨
∞—A£®©Å2£¨0£©∫ÕC£®0£¨3£©¥˙»Îy=m1x+n1£¨
µ√£∫ ![]() £¨
£¨
°‡Ω‚µ√ 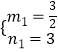 £¨
£¨
°‡÷±œflACµƒΩ‚Œˆ ΩŒ™£∫y= ![]() x+3£¨
x+3£¨
”…“‚÷™£∫QB=t£¨
»ÁÕº1£¨µ±°œNMQ=90°„£¨
°‡OQ=4©Åt£¨
¡Óx=4©Åt¥˙»Îy=©Å ![]() x+3£¨
x+3£¨
°‡y= ![]() t£¨
t£¨
°‡M£®4©Åt£¨ ![]() t£©£¨
t£©£¨
°flMN°Œx÷·£¨
°‡Nµƒ◊›◊¯±ÍŒ™ ![]() t£¨
t£¨
∞—y= ![]() t¥˙»Îy=
t¥˙»Îy= ![]() x+3£¨
x+3£¨
°‡x= ![]() t©Å2£¨
t©Å2£¨
°‡N£® ![]() t©Å2£¨
t©Å2£¨ ![]() t£©£¨
t£©£¨
°‡MN=£®4©Åt£©©Å£® ![]() t©Å2£©=6©Å
t©Å2£©=6©Å ![]() t£¨
t£¨
°flMQ°ŒOC£¨
°‡°˜BQM°◊°˜BOC£¨
°‡ ![]() £¨
£¨
°‡MQ= ![]() t£¨
t£¨
µ±MN=MQ ±£¨
°‡6©Å ![]() t=
t= ![]() t£¨
t£¨
°‡t= ![]() £¨
£¨
¥À ±QB= ![]() £¨∑˚∫œÃ‚“‚£¨
£¨∑˚∫œÃ‚“‚£¨
»ÁÕº2
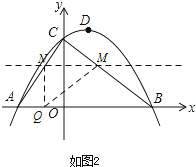
µ±°œQNM=90°„ ±£¨
°flQB=t£¨
°‡µ„Qµƒ◊¯±ÍŒ™£®4©Åt£¨0£©
°‡¡Óx=4©Åt¥˙»Îy= ![]() x+3£¨
x+3£¨
°‡y=9©Å ![]() t£¨
t£¨
°‡N£®4©Åt£¨9©Å ![]() t£©£¨
t£©£¨
°flMN°Œx÷·£¨
°‡µ„Mµƒ◊›◊¯±ÍŒ™9©Å ![]() t£¨
t£¨
°‡¡Óy=9©Å ![]() t¥˙»Îy=©Å
t¥˙»Îy=©Å ![]() x+3£¨
x+3£¨
°‡x=2t©Å8£¨
°‡M£®2t©Å8£¨9©Å ![]() t£©£¨
t£©£¨
°‡MN=£®2t©Å8£©©Å£®4©Åt£©=3t©Å12£¨
°flNQ°ŒOC£¨
°‡°˜AQN°◊°˜AOC£¨
°‡ ![]() £¨
£¨
°‡NQ=9©Å ![]() t£¨
t£¨
µ±NQ=MN ±£¨
°‡9©Å ![]() t=3t©Å12£¨
t=3t©Å12£¨
°‡t= ![]() £¨
£¨
°‡¥À ±QB= ![]() £¨∑˚∫œÃ‚“‚
£¨∑˚∫œÃ‚“‚
»ÁÕº3£¨
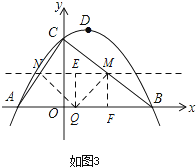
µ±°œNQM=90°„£¨
π˝µ„Q◊˜QE°ÕMN”⁄µ„E£¨
π˝µ„M◊˜MF°Õx÷·”⁄µ„F£¨
…ËQE=a£¨
¡Óy=a¥˙»Îy=©Å ![]() x+3£¨
x+3£¨
°‡x=4©Å ![]() a£¨
a£¨
°‡M£®4©Å ![]() a£¨a£©£¨
a£¨a£©£¨
¡Óy=a¥˙»Îy= ![]() x+3£¨
x+3£¨
°‡x= ![]() a©Å2£¨
a©Å2£¨
°‡N£® ![]() a©Å2£¨0£©£¨
a©Å2£¨0£©£¨
°‡MN=£®4©Å ![]() a£©©Å£®
a£©©Å£® ![]() a©Å2£©=6©Å2a£¨
a©Å2£©=6©Å2a£¨
µ±MN=2QE ±£¨
°‡6©Å2a=2a£¨
°‡a= ![]() £¨
£¨
°‡MF=QE= ![]() £¨
£¨
°flMF°ŒOC£¨
°‡°˜BMF°◊°˜BCO£¨
°‡ ![]() £¨
£¨
°‡BF=2£¨
°‡QB=QF+BF= ![]() +2=
+2= ![]() £¨
£¨
°‡t= ![]() £¨¥À«Èøˆ∑˚∫œÃ‚“‚£¨
£¨¥À«Èøˆ∑˚∫œÃ‚“‚£¨
◊€…œÀ˘ ˆ£¨µ±°˜QMNŒ™µ»—¸÷±Ω«»˝Ω«–Œ ±£¨¥À ±t= ![]() ªÚ
ªÚ ![]() ªÚ
ªÚ ![]() £Æ
£Æ
°æΩ‚Œˆ°ø±æÂøº≤È∂˛¥Œ∫Ø ˝µƒ◊€∫œŒ £¨…ʺ∞¥˝∂®œµ ˝∑®«Û“ª¥Œ∫Ø ˝∫Õ∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£¨œ‡À∆»˝Ω«–Œ≈–∂®”Ζ‘÷ £¨µ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ ÷™ ∂£¨“™ª·¿˚”√ ˝–ŒΩ·∫œµƒÀºœÎ∞—¥˙ ˝∫Õº∏∫ŒÕº–ŒΩ·∫œ∆¿¥£¨¿˚”√µ„µƒ◊¯±Íµƒ“‚“Â±Ì æœfl∂Œµƒ≥§∂»£¨¥”∂¯«Û≥ˆœfl∂Œ÷ƺ‰µƒπÿœµ£Æ£®1£©∑÷±¡Óy=0∫Õx=0¥˙»Îy=©Å ![]() x+3º¥ø…«Û≥ˆB∫ÕCµƒ◊¯±Í£¨»ª∫Û…Ë≈◊ŒÔœflµƒΩªµ„ ΩŒ™y=a£®x+2£©£®x©Å4£©£¨◊Ó∫Û∞—Cµƒ◊¯±Í¥˙»Î≈◊ŒÔœflΩ‚Œˆ Ωº¥ø…«Û≥ˆaµƒ÷µ∫Õ∂•µ„Dµƒ◊¯±Í£ª£®2£©»ÙÀƒ±fl–ŒDEFPŒ™∆Ω––Àƒ±fl–Œ ±£¨‘ÚDP°ŒBC£¨…Ë÷±œflDPµƒΩ‚Œˆ ΩŒ™y=mx+n£¨‘Úm=©Å
x+3º¥ø…«Û≥ˆB∫ÕCµƒ◊¯±Í£¨»ª∫Û…Ë≈◊ŒÔœflµƒΩªµ„ ΩŒ™y=a£®x+2£©£®x©Å4£©£¨◊Ó∫Û∞—Cµƒ◊¯±Í¥˙»Î≈◊ŒÔœflΩ‚Œˆ Ωº¥ø…«Û≥ˆaµƒ÷µ∫Õ∂•µ„Dµƒ◊¯±Í£ª£®2£©»ÙÀƒ±fl–ŒDEFPŒ™∆Ω––Àƒ±fl–Œ ±£¨‘ÚDP°ŒBC£¨…Ë÷±œflDPµƒΩ‚Œˆ ΩŒ™y=mx+n£¨‘Úm=©Å ![]() £¨«Û≥ˆ÷±œflDPµƒΩ‚Œˆ Ω∫Û£¨¡™¡¢≈◊ŒÔœflΩ‚Œˆ Ω∫Õ÷±œflDPµƒΩ‚Œˆ Ωº¥ø…«Û≥ˆPµƒ◊¯±Í£ª£®3£©”…“‚ø…÷™£¨0°‹t°‹6£¨»Ù°˜QMNŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨‘Úπ≤”–»˝÷÷«Èøˆ£¨¢Ÿ°œNMQ=90°„£ª¢⁄°œMNQ=90°„£ª¢€°œNQM=90°„£Æ
£¨«Û≥ˆ÷±œflDPµƒΩ‚Œˆ Ω∫Û£¨¡™¡¢≈◊ŒÔœflΩ‚Œˆ Ω∫Õ÷±œflDPµƒΩ‚Œˆ Ωº¥ø…«Û≥ˆPµƒ◊¯±Í£ª£®3£©”…“‚ø…÷™£¨0°‹t°‹6£¨»Ù°˜QMNŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨‘Úπ≤”–»˝÷÷«Èøˆ£¨¢Ÿ°œNMQ=90°„£ª¢⁄°œMNQ=90°„£ª¢€°œNQM=90°„£Æ
°æøºµ„æ´Œˆ°øΩ‚¥¥Àµƒπÿº¸‘⁄”⁄¿ÌΩ‚≈◊ŒÔœfl”Î◊¯±Í÷·µƒΩªµ„µƒœ‡πÿ÷™ ∂£¨’∆Œ’“ª‘™∂˛¥Œ∑Ω≥õƒΩ‚ «∆‰∂‘”¶µƒ∂˛¥Œ∫Ø ˝µƒÕºœÒ”Îx÷·µƒΩªµ„◊¯±Í£Æ“Ú¥À“ª‘™∂˛¥Œ∑Ω≥Ã÷–µƒb2-4ac£¨‘⁄∂˛¥Œ∫Ø ˝÷–±Ì æÕºœÒ”Îx÷· «∑Ò”–Ωªµ„£Æµ±b2-4ac>0 ±£¨ÕºœÒ”Îx÷·”–¡Ω∏ˆΩªµ„£ªµ±b2-4ac=0 ±£¨ÕºœÒ”Îx÷·”–“ª∏ˆΩªµ„£ªµ±b2-4ac<0 ±£¨ÕºœÒ”Îx÷·√ª”–Ωªµ„£Æ


 »´ƒ‹≤‚øÿ∆⁄ƒ©–°◊¥‘™œµ¡–¥∞∏
»´ƒ‹≤‚øÿ∆⁄ƒ©–°◊¥‘™œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº «≈◊ŒÔœfly=ax2+bx+c£®a°Ÿ0£©µƒ≤ø∑÷ÕºœÛ£¨∆‰∂•µ„◊¯±ÍŒ™£®1£¨n£©£¨«“”Îx÷·µƒ“ª∏ˆΩªµ„‘⁄µ„£®3£¨0£©∫Õ£®4£¨0£©÷ƺ‰£Æ‘Úœ¬¡–Ω·¬€£∫
¢Ÿa©Åb+c£æ0£ª
¢⁄3a+b=0£ª
¢€b2=4a£®c©Ån£©£ª
¢‹“ª‘™∂˛¥Œ∑Ω≥Ãax2+bx+c=n©Å1”–¡Ω∏ˆ≤ªœ‡µ»µƒ µ ˝∏˘£Æ
∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «£®°°°°£©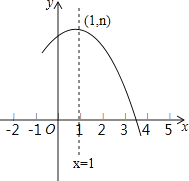
A.1
B.2
C.3
D.4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™£∫‘⁄∆Ω––Àƒ±fl–ŒABCD÷–£¨AB=2£¨AD=4£¨°œABC=60°„£¨EŒ™AD…œ“ªµ„£¨¡¨Ω”CE£¨AF°ŒCE«“ΩªBC”⁄µ„F£Æ
£®1£©«Û÷§£∫Àƒ±fl–ŒAECFŒ™∆Ω––Àƒ±fl–Œ£Æ
£®2£©÷§√˜£∫°˜AFB°’°˜CE D£Æ
£®3£©DEµ»”⁄∂‡…Ÿ ±£¨Àƒ±fl–ŒAECFŒ™¡‚–Œ£Æ
£®4£©DEµ»”⁄∂‡…Ÿ ±£¨Àƒ±fl–ŒAECFŒ™æÿ–Œ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() µ„D¥”µ„C≥ˆ∑¢—ÿCA∑ΩœÚ“‘√ø√Î2∏ˆµ•Œª≥§µƒÀŸ∂»œÚµ„A‘»ÀŸ‘À∂Ø£¨Õ¨ ±µ„E¥”µ„A≥ˆ∑¢—ÿAB∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§µƒÀŸ∂»œÚµ„B‘»ÀŸ‘À∂Ø£¨µ±∆‰÷–“ª∏ˆµ„µΩ¥Ô÷’µ„ ±£¨¡Ì“ª∏ˆµ„“≤ÀÊ÷ÆÕ£÷π‘À∂Ø£¨…˵„D°¢E‘À∂صƒ ±º‰ «t√Î
µ„D¥”µ„C≥ˆ∑¢—ÿCA∑ΩœÚ“‘√ø√Î2∏ˆµ•Œª≥§µƒÀŸ∂»œÚµ„A‘»ÀŸ‘À∂Ø£¨Õ¨ ±µ„E¥”µ„A≥ˆ∑¢—ÿAB∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§µƒÀŸ∂»œÚµ„B‘»ÀŸ‘À∂Ø£¨µ±∆‰÷–“ª∏ˆµ„µΩ¥Ô÷’µ„ ±£¨¡Ì“ª∏ˆµ„“≤ÀÊ÷ÆÕ£÷π‘À∂Ø£¨…˵„D°¢E‘À∂صƒ ±º‰ «t√Î![]() π˝µ„D◊˜
π˝µ„D◊˜![]() ”⁄µ„F£¨¡¨Ω”DE°¢EF£Æ
”⁄µ„F£¨¡¨Ω”DE°¢EF£Æ
![]() «Û÷§£∫
«Û÷§£∫![]() £ª
£ª
![]() Àƒ±fl–ŒAEFDƒ‹πª≥…Œ™¡‚–Œ¬£ø»Áπ˚ƒ‹£¨«Û≥ˆœ‡”¶µƒt÷µ£ª»Áπ˚≤ªƒ‹£¨Àµ√˜¿Ì”…£Æ
Àƒ±fl–ŒAEFDƒ‹πª≥…Œ™¡‚–Œ¬£ø»Áπ˚ƒ‹£¨«Û≥ˆœ‡”¶µƒt÷µ£ª»Áπ˚≤ªƒ‹£¨Àµ√˜¿Ì”…£Æ
![]() µ±tŒ™∫Œ÷µ ±£¨
µ±tŒ™∫Œ÷µ ±£¨![]() Œ™÷±Ω«»˝Ω«–Œ£ø«ÎÀµ√˜¿Ì”…£Æ
Œ™÷±Ω«»˝Ω«–Œ£ø«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–![]() ÷±œfl
÷±œfl![]() ”Îx÷·°¢y÷·œ‡Ωª”⁄A°¢B¡Ωµ„£¨∂ص„C‘⁄œfl∂ŒOA…œ£¨Ω´œfl∂ŒCB»∆◊≈µ„CÀ≥ ±’Ζ˝◊™
”Îx÷·°¢y÷·œ‡Ωª”⁄A°¢B¡Ωµ„£¨∂ص„C‘⁄œfl∂ŒOA…œ£¨Ω´œfl∂ŒCB»∆◊≈µ„CÀ≥ ±’Ζ˝◊™![]() µ√µΩCD£¨¥À ±µ„D«°∫√¬‰‘⁄÷±œflAB…œ ±£¨π˝µ„D◊˜
µ√µΩCD£¨¥À ±µ„D«°∫√¬‰‘⁄÷±œflAB…œ ±£¨π˝µ„D◊˜![]() ÷·”⁄µ„E£Æ
÷·”⁄µ„E£Æ
![]() «Û÷§£∫
«Û÷§£∫![]() °’
°’![]() £ª
£ª
![]() »ÁÕº2£¨Ω´
»ÁÕº2£¨Ω´![]() —ÿx÷·’˝∑ΩœÚ∆Ω“∆µ√
—ÿx÷·’˝∑ΩœÚ∆Ω“∆µ√![]() £¨µ±÷±œfl
£¨µ±÷±œfl![]() æ≠π˝µ„D ±£¨«Ûµ„Dµƒ◊¯±Íº∞
æ≠π˝µ„D ±£¨«Ûµ„Dµƒ◊¯±Íº∞![]() ∆Ω“∆µƒæ‡¿Î£ª
∆Ω“∆µƒæ‡¿Î£ª
![]() »Ùµ„P‘⁄y÷·…œ£¨µ„Q‘⁄÷±œflAB…œ
»Ùµ„P‘⁄y÷·…œ£¨µ„Q‘⁄÷±œflAB…œ![]() «∑ҥʑ⁄“‘C°¢D°¢P°¢QŒ™∂•µ„µƒÀƒ±fl–Œ «∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒQµ„◊¯£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
«∑ҥʑ⁄“‘C°¢D°¢P°¢QŒ™∂•µ„µƒÀƒ±fl–Œ «∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨÷±Ω”–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒQµ„◊¯£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™»ÁÕº£¨AD°ŒBC£¨AB°ÕBC£¨CD°ÕDE£¨CD=ED£¨AD=2£¨BC=3£¨‘Ú°˜ADEµƒ√ʪ˝Œ™£® £©

A.1 B.2 C.5 D.Œfi∑®»∑∂®
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°œBAD=°œCAE=90°„£¨AB=AD£¨AE=AC£¨AF°ÕCB£¨¥π◊„Œ™F£Æ
£®1£©«Û÷§£∫°˜ABC°’°˜ADE£ª
£®2£©«Û°œFAEµƒ∂» ˝£ª
£®3£©«Û÷§£∫CD=2BF+DE£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº∆À„œ¬¡–≤ªµ» Ω£®◊È£©£∫
£®1£©x-![]() £º2-
£º2-![]() .
.
£®2£©-2°‹![]() °‹7
°‹7
£®3£©![]() £ª
£ª
£®4£©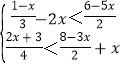
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœfly=x2+bx”Î÷±œfly=2x+4Ωª”⁄A£®a£¨8£©°¢B¡Ωµ„£¨µ„P «≈◊ŒÔœfl…œA°¢B÷ƺ‰µƒ“ª∏ˆ∂ص„£¨π˝µ„P∑÷±◊˜x÷·°¢y÷·µƒ∆Ω––œfl”Î÷±œflABΩª”⁄µ„C∫Õµ„E£Æ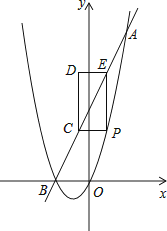
£®1£©«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®2£©»ÙCŒ™AB÷–µ„£¨«ÛPCµƒ≥§£ª
£®3£©»ÁÕº£¨“‘PC£¨PEŒ™±flππ‘Ïæÿ–ŒPCDE£¨…˵„Dµƒ◊¯±ÍŒ™£®m£¨n£©£¨«Î«Û≥ˆm£¨n÷ƺ‰µƒπÿœµ Ω£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com