
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )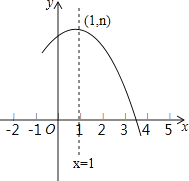
A.1
B.2
C.3
D.4
【答案】C
【解析】解:∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣2,0)和(﹣1,0)之间.
∴当x=﹣1时,y>0,
即a﹣b+c>0,所以①正确;
∵抛物线的对称轴为直线x=﹣ ![]() =1,即b=﹣2a,
=1,即b=﹣2a,
∴3a+b=3a﹣2a=a,所以②错误;
∵抛物线的顶点坐标为(1,n),
∴ ![]() =n,
=n,
∴b2=4ac﹣4an=4a(c﹣n),所以③正确;
∵抛物线与直线y=n有一个公共点,
∴抛物线与直线y=n﹣1有2个公共点,
∴一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.
故选C.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】数轴上点 A,B 到表示2 的点的距离都为 9,P 为线段 AB 上任一点,C,D 两点分别从 P,B 同时向 A 点移动,且 C 点运动速度为每秒 3 个单位长度,D 点运动速度为每秒 4 个单位长度,运动 3 秒时,CD=4,则 P 点表示的数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
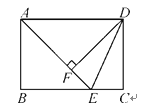
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由组成的图案和算式,解答问题:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算 1+3+5+7+9+11;
(2)请计算 1+3+5+7+9+…+19;
(3)请计算 1+3+5+7+9+…+(2n﹣1);
(4)请用上述规律计算:21+23+25+…+99.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种“24 点”游戏,其游戏规则是:任取一副扑克牌,我们约定A 为 1,J,Q,K 分别为 11、12、13,并规定红色牌为正,黑色牌为负,任取 4 张牌,将这 4 张牌的牌面所表示的数进行加减乘除四则运算(每个数用且只用 1 次),使其结果等于 24.
例如,取 4 张牌为:红桃 A,红桃 2,方块 3,方块 4,可作运算(1+2+3)×4 =24.
[注意上述运算与 4×(1+2+3)=24 应视作相同方法的运算]
现有 4 张扑克牌分别为红桃 3、黑桃 6、方块 4、方块 10,运用上述规则写出 3种不同的运算式:
(1) ;
(2) ;
(3) .
(4)另有 4 张扑克牌分别为红桃 3,黑桃 5,梅花 J,方块 7,可通过运算式 ,使其结果等于 24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图像提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次过C点到第二次过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
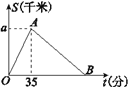
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象经过点A(6,﹣3)和点B(﹣2,5).
(1)求这个一次函数的表达式.
(2)求该函数图象与坐标轴围成的三角形的面积.
(3)判断点C(2,2)是在直线AB的上方(右边)还是下方(左边).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标为(﹣2,0),直线y=﹣ ![]() x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点.
x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点. 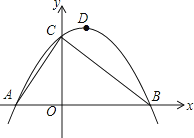
(1)请直接写出B、C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com