
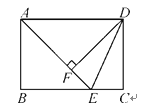
【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由矩形的性质得出对边相等,对边平行,四个角为90°,然后由平行线的性质得出∠AEB=∠DAF,根据AAS可证得△ABE≌△DFA,根据全等三角形的对应边相等即可得出结论;
(2)利用HL证明Rt△DFE≌Rt△DCE即可得出结论.
(1)∵四边形ABCD是长方形,
∴AD=BC,AD∥BC,∠B=∠C=90°,
∴∠AEB=∠DAF.
又AE=BC,
∴AE=AD.
∵DF⊥AE,
∴∠DFA =90° =∠B,
在△ABE和△DFA中,
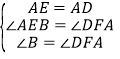
∴△ABE≌△DFA(AAS),
∴AB=DF;
(2)∵AB=DF,AB=DC,
∴DF=DC.
又DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴∠DEF=∠DEC,
即DE平分∠AEC.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
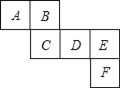
【题目】如图是一个正方体的表面展开图,请回答下列问题:
(1)与面B、C相对的面分别是 ;
(2)若A=a3+a2b+3,B=a2b﹣3,C=a3﹣1,D=﹣(a2b﹣6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某景区的环形游览路线ABCDA,已知从景点C到出口A的两条道路CBA和CDA均为1600米,现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形道路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车的速度均为200米/分,每一个游客的步行速度均为50米/分.

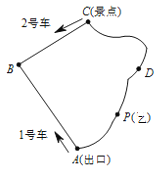

(1)探究(填空):
①当两车行驶 分钟时,1、2号车第一次相遇,此相遇点到出口A的路程为 米;
②当1号车第二次恰好经过点C,此时两车行驶了 分钟,这一段时间内1号车与2号车相遇了 次.
(2)发现:
若游客甲在BC上K处(不与点C、B重合)候车,准备乘车到出口A,在下面两种情况下,请问哪种情况用时较少(含候车时间)?请说明理由.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
(3)决策:
①若游客乙在DA上从D向出口A走去,游客乙从D出发时恰好2号车在C处,当步行到DA上一点P(不与A,D重合)时,刚好与2号车相遇,经计算他发现:此时原地(P点)等候乘1号车到出口与直接从P步行到达出口A这两种方式,所花时间相等,请求出D点到出口A的路程.
②当游客丙逛完景点C后准备到出口A,此时2号车刚好在B点,已知BC路程为600米,请你帮助游客丙做一下决策,怎样到出口A所花时间最少,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,…每个正方形四条边上的整点的个数.按此规律推算出正方形A2 016B2 016C2 016D2 016四条边上的整点共有_________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场苹果的价格如下表:
购买苹果 | 不超过20千克的部分 | 超过20千克但不超出40千克的部分 | 超出40千克的部分 |
每千克的价格 | 6元 | 5元 | 4元 |
(1)小明第一次购买苹果10千克,需要付费多少元;
小明第二次购买苹果![]() 千克(
千克(![]() 超过20千克但不超过40千克),需要付费多少元(用含
超过20千克但不超过40千克),需要付费多少元(用含![]() 的式子表示);
的式子表示);
(2)小强分两次共购买100千克,第二次购买的数量多于第一次购买的数量,且第一次购买的数量为![]() 千克,请问小强两次购买苹果共需要付费多少元?(用含
千克,请问小强两次购买苹果共需要付费多少元?(用含![]() 的式子表示);
的式子表示);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )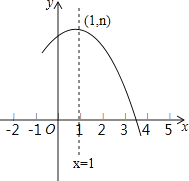
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在平行四边形ABCD中,AB=2,AD=4,∠ABC=60°,E为AD上一点,连接CE,AF∥CE且交BC于点F.
(1)求证:四边形AECF为平行四边形.
(2)证明:△AFB≌△CE D.
(3)DE等于多少时,四边形AECF为菱形.
(4)DE等于多少时,四边形AECF为矩形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com