
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
【答案】
(1)
解:设第一批T恤衫每件进价是x元,则第二批每件进价是(x﹣10)元,根据题意可得: ![]() ,
,
解得:x=150,
经检验x=150是原方程的解,
答:第一批T恤衫每件进价是150元,第二批每件进价是140元,
![]() (件),
(件), ![]() (件),
(件),
答:第一批T恤衫进了30件,第二批进了15件
(2)
解:设第二批衬衫每件售价y元,根据题意可得:
30×(200﹣150)+15(y﹣140)≥1950,
解得:y≥170,
答:第二批衬衫每件至少要售170元
【解析】(1)设第一批T恤衫每件进价是x元,则第二批每件进价是(x﹣10)元,再根据等量关系:第二批进的件数= ![]() ×第一批进的件数可得方程;(2)设第二批衬衫每件售价y元,由利润=售价﹣进价,根据这两批衬衫售完后的总利润不低于1950元,可列不等式求解.本题考查分式方程、一元一次不等式的应用,关键是根据数量作为等量关系列出方程,根据利润作为不等关系列出不等式求解.
×第一批进的件数可得方程;(2)设第二批衬衫每件售价y元,由利润=售价﹣进价,根据这两批衬衫售完后的总利润不低于1950元,可列不等式求解.本题考查分式方程、一元一次不等式的应用,关键是根据数量作为等量关系列出方程,根据利润作为不等关系列出不等式求解.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:
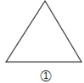
【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为![]() 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
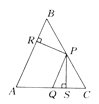
A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
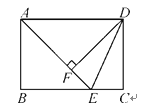
【题目】如图,在长方形ABCD中,点E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)求证:DE平分∠AEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.

解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线![]() :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种“24 点”游戏,其游戏规则是:任取一副扑克牌,我们约定A 为 1,J,Q,K 分别为 11、12、13,并规定红色牌为正,黑色牌为负,任取 4 张牌,将这 4 张牌的牌面所表示的数进行加减乘除四则运算(每个数用且只用 1 次),使其结果等于 24.
例如,取 4 张牌为:红桃 A,红桃 2,方块 3,方块 4,可作运算(1+2+3)×4 =24.
[注意上述运算与 4×(1+2+3)=24 应视作相同方法的运算]
现有 4 张扑克牌分别为红桃 3、黑桃 6、方块 4、方块 10,运用上述规则写出 3种不同的运算式:
(1) ;
(2) ;
(3) .
(4)另有 4 张扑克牌分别为红桃 3,黑桃 5,梅花 J,方块 7,可通过运算式 ,使其结果等于 24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 P是线段 AB上的一点,![]() ,C, D两点从 A, P同时出发,分别以2
,C, D两点从 A, P同时出发,分别以2 ![]() ,1
,1![]() 的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=
的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=![]()
![]() ,点 C,D的运动时间为
,点 C,D的运动时间为![]() .
.
(1)用含![]() 和 的代数式表示线段 CP 的长度.
和 的代数式表示线段 CP 的长度.
(2)当 t =5时,![]() ,求线段 AB的长.
,求线段 AB的长.
(3)当 BC-AC=PC时,求 ![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com