
分析 根据红棋共有16个,“炮”有4个,黑“马”2个,红“兵”5个,再由概率公式即可得出结论.
解答 解:∵一副中国象棋(32枚),红棋共有16个,“炮”有4个,黑“马”2个,红“兵”5个,
∴从中随机摸出一枚棋子,摸得红棋的概率=$\frac{16}{32}$=$\frac{1}{2}$;
摸得“炮”的概率=$\frac{4}{32}$=$\frac{1}{8}$;
摸得黑“马”的概率=$\frac{2}{32}$=$\frac{1}{16}$;
摸得红“兵”的概率=$\frac{5}{32}$.
故答案为:$\frac{1}{2}$,$\frac{1}{8}$,$\frac{1}{16}$,$\frac{5}{32}$.
点评 本题考查的是概率公式,熟记概率=所求情况数与总情况数之比是解答此题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
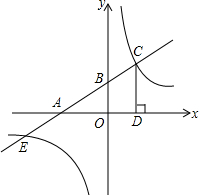 已知直线l1:y1=$\frac{1}{2}$x+2分别交x轴,y轴于点A、B,点C是该直线上在第一象限内的一点,作CD⊥x轴于点D,使得S△ACD=9,再过点C作一条双曲线y2=$\frac{k}{x}$
已知直线l1:y1=$\frac{1}{2}$x+2分别交x轴,y轴于点A、B,点C是该直线上在第一象限内的一点,作CD⊥x轴于点D,使得S△ACD=9,再过点C作一条双曲线y2=$\frac{k}{x}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直线CD上有一动点P,P在CD上从右往左运动的过程中,找出:
如图,在直线CD上有一动点P,P在CD上从右往左运动的过程中,找出:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com