
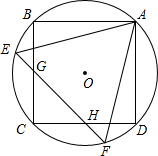
 如图所示,已知正方形ABCD和正△AEF都内接于圆,EF与BC和CD分别交于G、H,则GH:EF=$\sqrt{3}$:3.
如图所示,已知正方形ABCD和正△AEF都内接于圆,EF与BC和CD分别交于G、H,则GH:EF=$\sqrt{3}$:3. 分析 设⊙O的半径是r,则OF=r,根据AO是∠EAF的平分线,求出∠COF=60°,在Rt△OIF中,求出FI的值是多少;然后判断出OI、CI的关系,再根据GH∥BD,求出GH的值,求出比值即可
解答 解:如图,连接AC、BD、OF,AC交EF于I,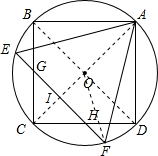
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴COF=30°+30°=60°,
∴FI=r•sin60°=$\frac{\sqrt{3}}{2}$r,
∴EF=$\frac{\sqrt{3}}{2}$r×2=$\sqrt{3}$r,
∵AO=2OI,
∴OI=$\frac{1}{2}$r,CI=r-$\frac{1}{2}$r=$\frac{1}{2}$r,
∴$\frac{GH}{BD}$=$\frac{CI}{CO}$=$\frac{1}{2}$,
∴GH=r,
∴GH:EF=$\sqrt{3}$:3.
故答案为:$\sqrt{3}$:3.
点评 此题主要考查了正多边形与圆的关系,要熟练掌握,解答此题的关键是要明确正多边形的有关概念:①中心:正多边形的外接圆的圆心叫做正多边形的中心.②正多边形的半径:外接圆的半径叫做正多边形的半径.③中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.④边心距:中心到正多边形的一边的距离叫做正多边形的边心距.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
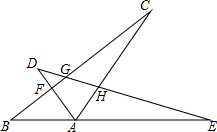 如图,在△ABC中,∠BAC=120°,将△ABC绕点A顺时针旋转60°得△ADE,则图中有3对全等三角形,它们是△ADE≌△ABC,BAF≌△DAH,△AEH≌△ACF.
如图,在△ABC中,∠BAC=120°,将△ABC绕点A顺时针旋转60°得△ADE,则图中有3对全等三角形,它们是△ADE≌△ABC,BAF≌△DAH,△AEH≌△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.
如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,AD∥BC,BA,CD的延长线相交于点E,若AD=2,BC=3,BA=2.5,则AE=5,理由是:相似三角形的性质.
如图,四边形ABCD中,AD∥BC,BA,CD的延长线相交于点E,若AD=2,BC=3,BA=2.5,则AE=5,理由是:相似三角形的性质.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式.
现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com