
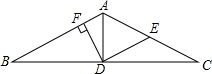
 如图,在△ABC中,AB=AC,AD是△ABC点的中线,E是AC的中点,连接AC,DF⊥AB于F.求证:∠BDF=∠ADE.
如图,在△ABC中,AB=AC,AD是△ABC点的中线,E是AC的中点,连接AC,DF⊥AB于F.求证:∠BDF=∠ADE. 分析 根据等腰三角形的性质得到∠BAD=∠CAD,∠ADB=∠ADC=90°,根据等腰三角形的判定定理得到∠CAD=∠ADE.根据余角的性质得到∠BAD=∠BDF,等量代换即可得到结论.
解答 证明:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD,∠ADB=∠ADC=90°,
∵E是AC的中点,
∴DE=AE=EC,
∴∠CAD=∠ADE.
在Rt△ABD中,∠ADB=90°,
∴∠B+∠BAD=90°.
∵DF⊥AB,
∴∠B+∠BDF=90°,
∴∠BAD=∠BDF,
∴∠BDF=∠CAD,
∴∠BDF=∠ADE.
点评 本题考查了等腰直角三角形的性质,余角的性质,熟练掌握等腰三角形的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)| 分组 | 频数 | 频率 |
| 156.5~161.5 | 3 | 0.15 |
| 161.5~166.5 | 2 | 0.10 |
| 166.5~171.5 | 4 | |
| 171.5~176.5 | 0.30 | |
| 176.5~181.5 | ||
| 合计 | 20 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上.
在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )
如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )| A. | 155° | B. | 130° | C. | 125° | D. | 110° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com