
 如图,在△ABC 中,AC=24cm,BC=7cm,AB=25cm,P 点在 BC 上从 B 点到 C 点 运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A 点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索的主要过程.
如图,在△ABC 中,AC=24cm,BC=7cm,AB=25cm,P 点在 BC 上从 B 点到 C 点 运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A 点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索的主要过程.分析 (1)根据勾股定理PC2+CQ2=PQ2,便可求出经过1s后,P、Q两点的距离为5$\sqrt{2}$cm2
(2)根据三角形的面积公式S△PCQ=$\frac{1}{2}$×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2
(3)根据三角形的面积公式S△PCQ=$\frac{1}{2}$×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大.
解答 解:(1)设经过ts后,P、Q两点的距离为5$\sqrt{2}$cm,
ts后,PC=7-2t cm,CQ=5t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(7-2t)2+(5t)2=(5$\sqrt{2}$)2;
解得t=1或t=-$\frac{1}{29}$(不合题意舍去);
(2)设经过ts后,S△PCQ的面积为15cm2
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=$\frac{1}{2}$×PC×CQ=$\frac{1}{2}$×(7-2t)×5t=15
解得t1=2,t2=1.5,
经过2或1.5s后,S△PCQ的面积为15cm2
(3)设经过ts后,△PCQ的面积最大,
ts后,PC=7-2t cm,CQ=5t cm,
S△PCQ=$\frac{1}{2}$×PC×CQ=$\frac{1}{2}$×(7-2t)×5t=$\frac{5}{2}$×(-2t2+7t)
当t=-$\frac{b}{2a}$时,即t=$\frac{7}{2×2}$=1.75s时,△PCQ的面积最大,
即S△PCQ=$\frac{1}{2}$×PC×CQ=$\frac{1}{2}$×(7-2×1.75)×5×1.752=$\frac{245}{16}$.
当时间为1.75秒时,最大面积为$\frac{245}{16}$.
点评 此题考查一元二次方程的应用和配方法法的应用,注意与勾股定理相结合求得相关线段的长度,是各地中考的热点,属于中档题.


科目:初中数学 来源: 题型:解答题
 已知两个分别含有30°,45°角的一副直角三角板.
已知两个分别含有30°,45°角的一副直角三角板.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 表示-x的平方的式子是-x2 | B. | 表示x、y2、3$\frac{1}{2}$的积的式子是3$\frac{1}{2}$xy2 | ||
| C. | x、y两数差的平方表示为(x-y)2 | D. | x2+y2的意义是x与y和的平方 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
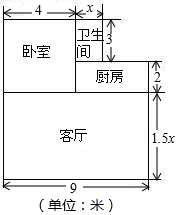 一家住房的地面结构如图所示,请根据图中的数据,解答下列问题:
一家住房的地面结构如图所示,请根据图中的数据,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
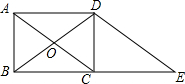 如图,在矩形ABCD中,AB=2,AD=3,对角线AC、BD相交于点O,过点D作DE∥AC交BC延长线于点E.
如图,在矩形ABCD中,AB=2,AD=3,对角线AC、BD相交于点O,过点D作DE∥AC交BC延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com