
分析 根据题意画出图形,由平行四边形的性质可得AO=CO=$\frac{1}{2}$AC,BO=DO=$\frac{1}{2}$BD,AD=BC,DC=AB,根据平行四边形周长等于70cm可得AB+BC=35cm,然后再设出AC=3xcm,BD=2xcm,根据两个相邻的三角形的周长和等于80cm列出方程,解出x的值,进而可得答案.
解答 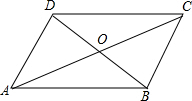 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AO=CO=$\frac{1}{2}$AC,BO=DO=$\frac{1}{2}$BD,AD=BC,DC=AB,
∵平行四边形周长等于70cm,
∴AB+BC=35cm,
设AC=3xcm,BD=2xcm,
则3x+x+x+35=80,
解得:x=9,
AC=27cm,BD=18cm,
答:两条对角线的长度为27cm和18cm.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形对边相等,对角线互相平分.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
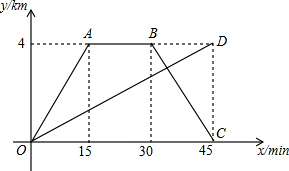 甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)
甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠C=90°.E为AB中点,D为AC上一点,BF∥AC交DE的延长线于点F.AC=6,BC=5.则四边形FBCD周长的最小值是16.
如图,Rt△ABC中,∠C=90°.E为AB中点,D为AC上一点,BF∥AC交DE的延长线于点F.AC=6,BC=5.则四边形FBCD周长的最小值是16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,分别以它的三边为边长,在BC边的同侧作三个等边三角形,即△ABD,△BCE,△ACF,求证:四边形ADEF是平行四边形.
如图,已知△ABC,分别以它的三边为边长,在BC边的同侧作三个等边三角形,即△ABD,△BCE,△ACF,求证:四边形ADEF是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ACB中,∠ACB=90°,点D为BC边上的一点,将线段BD绕点B顺时针方向旋转(点E与点D对应),当BD旋转至与AB垂直时,点A,D,E恰好在同一直线上,作EF⊥BC于点F.若$\frac{CD}{DF}$=$\frac{3}{2}$,AE=5$\sqrt{5}$,则线段AB的长度为10.
如图,在Rt△ACB中,∠ACB=90°,点D为BC边上的一点,将线段BD绕点B顺时针方向旋转(点E与点D对应),当BD旋转至与AB垂直时,点A,D,E恰好在同一直线上,作EF⊥BC于点F.若$\frac{CD}{DF}$=$\frac{3}{2}$,AE=5$\sqrt{5}$,则线段AB的长度为10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC为等边三角形,点D为BC边上的中点,DF⊥AB于点F,点E在BA的延长线上,且ED=EC,若AE=2,则AF的长为( )
如图,△ABC为等边三角形,点D为BC边上的中点,DF⊥AB于点F,点E在BA的延长线上,且ED=EC,若AE=2,则AF的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$+1 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com