
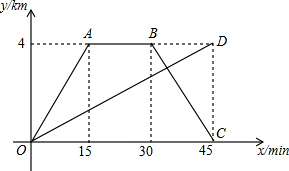
 甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)
甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)分析 (1)设出设甲距学校的距离y与甲离开学校的时间x的函数关系式为y=kx+b,结合图象中的点,分段利用待定系数法即可得出结论;
(2)结合图象求出乙距学校的距离y与乙离开学校的时间x的函数关系式为,令甲关系式-乙关系式=2再结合图象即可得出结论.
解答 解:(1)设甲距学校的距离y与甲离开学校的时间x的函数关系式为y=kx+b,
当0≤x≤15时,有$\left\{\begin{array}{l}{0=b}\\{4=15k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{4}{15}}\\{b=0}\end{array}\right.$,
此时y=$\frac{4}{15}$x;
当15<x≤30时,y=4;
当30<x≤45时,有$\left\{\begin{array}{l}{4=30k+b}\\{0=45k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{4}{15}}\\{b=12}\end{array}\right.$,
此时y=-$\frac{4}{15}$x+12.
综上得:甲距学校的距离y与甲离开学校的时间x的函数关系式y=$\left\{\begin{array}{l}{\frac{4}{15}x(0≤x≤15)}\\{4(15<x≤30)}\\{-\frac{4}{15}+12(30<x≤45)}\end{array}\right.$.
(2)设乙距学校的距离y与乙离开学校的时间x的函数关系式为y=ax+c,根据题意可知:
$\left\{\begin{array}{l}{0=c}\\{4=45a+c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{4}{45}}\\{c=0}\end{array}\right.$,
即乙距学校的距离y与乙离开学校的时间x的函数关系式为y=$\frac{4}{45}$x.
当0≤x≤15时,令$\frac{4}{15}$x-$\frac{4}{45}$x=2,
解得:x=$\frac{45}{4}$;
当15<x≤30时,令4-$\frac{4}{45}$x=2,
解得:x=$\frac{45}{2}$;
当30<x≤45时,结合图象可知,此时不存在符合题意得x.
综上可知:在两人相遇前,甲离开学校$\frac{45}{4}$分钟和$\frac{45}{2}$分钟时与乙相距2km.
点评 本题考查了一次函数应用中的相遇问题以及用待定系数法求一次函数的解析式,解题的关键是(1)利用待定系数法求出解析式;(2)紧密结合图象,利用数形结合找出结论.本题属于中档题型,难度不大,但在计算过程中注意数形结合,以及理清题意.


科目:初中数学 来源: 题型:选择题
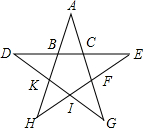 某公司要在如图所示的五角星(∠A=∠D=∠H=∠G=∠E=36°,AB=AC=CE=EF=FG=GI=HI=HK=DK=DB)中,沿边每隔25厘米装一盏闪光灯,若BC=($\sqrt{5}$-1)米,则需要安装闪光灯( )
某公司要在如图所示的五角星(∠A=∠D=∠H=∠G=∠E=36°,AB=AC=CE=EF=FG=GI=HI=HK=DK=DB)中,沿边每隔25厘米装一盏闪光灯,若BC=($\sqrt{5}$-1)米,则需要安装闪光灯( )| A. | 79盏 | B. | 80盏 | C. | 81盏 | D. | 82盏 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,点D在AC边上,AD=$\frac{3}{2}$CD,在$\widehat{BC}$上取一点E,使得∠CDE=∠ABC,连接AE,求$\frac{AE}{DE}$的值.
如图,△ABC内接于⊙O,点D在AC边上,AD=$\frac{3}{2}$CD,在$\widehat{BC}$上取一点E,使得∠CDE=∠ABC,连接AE,求$\frac{AE}{DE}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OM与OB是两坐标轴夹角的三等分线,点E是OM上一点,EC⊥x轴于C点,ED⊥OB于D点.(1)求证:∠ECD=∠EDC;
如图,OM与OB是两坐标轴夹角的三等分线,点E是OM上一点,EC⊥x轴于C点,ED⊥OB于D点.(1)求证:∠ECD=∠EDC;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com