
分析 先把方程组转化成二元一次方程,根据根的判别式得出△≥0,求出不等式的解集即可.
解答 解:$\left\{\begin{array}{l}{{x}^{2}+xy+9{y}^{2}=1①}\\{x-3y=k②}\end{array}\right.$
由②得:x=k+3y,③
把③代入②得:(k+3y)2+(k+3y)y+9y2=1,
即21y2+7ky+k2-1=0,
∵方程组$\left\{\begin{array}{l}{{x}^{2}+xy+{9y}^{2}=1}\\{x-3y=k}\end{array}\right.$有实数解,
∴△=(7k)2-4×21×(k2-1)≥0,
解得:-$\frac{2\sqrt{15}}{2}$≤k≤$\frac{2\sqrt{15}}{5}$,
即实数k的取值范围是-$\frac{2\sqrt{15}}{2}$≤k≤$\frac{2\sqrt{15}}{5}$.
点评 本题考查了高次方程,根的判别式的应用,能得出不等式是解此题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| 成绩(分) | 78 | 89 | 96 | 100 |
| 人数 | 1 | 2 | 3 | 1 |
| A. | 22 | B. | 89 | C. | 92 | D. | 96 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
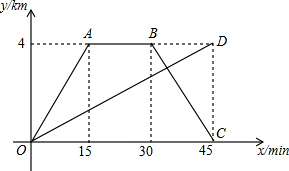 甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)
甲、乙两人同时从学校出发,沿相同路线前往书店,甲骑自行车,乙步行,当甲到书店购书后按原路回到学校时,乙恰好到达书店,图中折线OABC和线段OD分别表示甲、乙两人距学校的距离y(km)与甲离开学校的时间x(min)的函数图象(假设甲骑自行车、乙步行的速度均不变)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -11 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,边长为3的正△ABC内接于⊙O,点P是$\widehat{AB}$上的动点,则PA+PB的最大值是( )
如图,边长为3的正△ABC内接于⊙O,点P是$\widehat{AB}$上的动点,则PA+PB的最大值是( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{3}{2}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ACB中,∠ACB=90°,点D为BC边上的一点,将线段BD绕点B顺时针方向旋转(点E与点D对应),当BD旋转至与AB垂直时,点A,D,E恰好在同一直线上,作EF⊥BC于点F.若$\frac{CD}{DF}$=$\frac{3}{2}$,AE=5$\sqrt{5}$,则线段AB的长度为10.
如图,在Rt△ACB中,∠ACB=90°,点D为BC边上的一点,将线段BD绕点B顺时针方向旋转(点E与点D对应),当BD旋转至与AB垂直时,点A,D,E恰好在同一直线上,作EF⊥BC于点F.若$\frac{CD}{DF}$=$\frac{3}{2}$,AE=5$\sqrt{5}$,则线段AB的长度为10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com