
【题目】观察下列各式及其验证过程:![]() ,验证:
,验证:![]() .
.![]() , 验证:
, 验证:![]() .
.
(1)按照上述两个等式及其验证过程,猜想![]() 的变形结果并进行验证.
的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用a(a为任意自然数,且a≥2)表示的等式,并给出验证.
(3)针对三次根式及n次根式(n为任意自然数,且n≥2),有无上述类似的变形?如果有,写出用a(a为任意自然数,且a≥2)表示的等式,并给出验证.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,点![]() 的坐标为
的坐标为![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位得到点
个单位得到点![]() ,其中关于
,其中关于![]() 的一元一次不等式
的一元一次不等式![]() 的解集为
的解集为![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() .
.
(1)求![]() 两点坐标及四边形
两点坐标及四边形![]() 的面积;
的面积;
(2)如图2,点![]() 自
自![]() 点以1个单位/秒的速度在
点以1个单位/秒的速度在![]() 轴上向上运动,点
轴上向上运动,点![]() 自
自![]() 点以2个单位/秒的速度在
点以2个单位/秒的速度在![]() 轴上向左运动,设运动时间为
轴上向左运动,设运动时间为![]() 秒(
秒(![]() ),是否存在一段时间使得
),是否存在一段时间使得![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)在(2)的条件下,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务;全等四边形根据全等图形的定又可知:四条边分别相等、四个角也分别相等的两个四边形全等。在“探索三角形全等的条件”时,我们把两个三角形中“一条边和等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”,进行了如下思考:如图1,四边形![]() 和四边形
和四边形![]() 中,连接对角线
中,连接对角线![]() ,这样两个四边形全等的问题就转化为“
,这样两个四边形全等的问题就转化为“![]() ”与“
”与“![]() ”的问题。若先给定“
”的问题。若先给定“![]() ”的条件,只要再增加
”的条件,只要再增加![]() 个条件使“
个条件使“![]() ”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
按照智慧小组的思路,小明对图![]() 中的四边形
中的四边形![]() 与四边形
与四边形![]() 先给出和下条件:
先给出和下条件: ![]() ,
,![]() ,小亮在此基础上又给出“
,小亮在此基础上又给出“![]() ”两个条件.他们认为满足这五个条件能得到“四边形
”两个条件.他们认为满足这五个条件能得到“四边形![]() 四边形
四边形![]() ”.
”.

(1)请根据小明和小亮给出的条件,说明“四边形![]() 四边形
四边形![]() ”的理由;
”的理由;
(2)请从下面![]() 两题中任选一题作答,我选择 题.
两题中任选一题作答,我选择 题.
![]() 在材料中“小明所给条件”的基础上,小颖又给出两个条件“
在材料中“小明所给条件”的基础上,小颖又给出两个条件“![]() ”.满足这五个条件 (填“能”或“不能”)得到四边形
”.满足这五个条件 (填“能”或“不能”)得到四边形![]() 四边形
四边形![]()
![]() 在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形
在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形![]() 四边形
四边形![]() ,你添加的条件是① ,② .
,你添加的条件是① ,② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人寿保险公司的一张关于某地区的生命表的部分摘录如下:
年龄 | 活到该年龄的人数 | 在该年龄的死亡人数 |
40 | 80500 | 892 |
50 | 78009 | 951 |
60 | 69891 | 1200 |
70 | 45502 | 2119 |
80 | 16078 | 2001 |
… | … | … |
根据上表解下列各题:
(1)某人今年50岁,他当年去世的概率是多少?他活到80岁的概率是多少?
(保留三个有效数字)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需付赔偿的总额为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.
(1) 求a、b的值;
(2) 若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?
(3) 在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一 种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
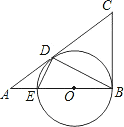
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形△ABC中,D是BC边的中点,AD=![]() BC.
BC.
(1)△ABC的形状为 .
(2)如图,BM=3,BC=12,∠B=45°,∠MAN=45°,求CN;
(3)在(2)的条件下,AN= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com