
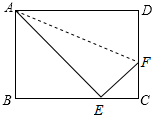
 如图,折叠矩形ABCD的一边AD使点D落在BC边上的E处,已知折痕AF=10cm,且tan∠FEC=$\frac{3}{4}$.
如图,折叠矩形ABCD的一边AD使点D落在BC边上的E处,已知折痕AF=10cm,且tan∠FEC=$\frac{3}{4}$.分析 (1)在Rt△EFC中利用三角函数定义得tan∠FEC=$\frac{FC}{EC}$=$\frac{3}{4}$,则可设FC=3k,EC=4k,利用勾股定理可计算得EF=5k,再根据折叠的性质得DF=EF=5k,AD=AE,∠AEF=∠D=90°,则DC=DF+CF=8k,于是AB=CD=8k,利用等角的余角相等得到∠BAE=∠FEC,接着在Rt△ABE中,利用正切的定义得到BE=6k,则利用勾股定理可得AE=10k,所以AD=10k,然后在Rt△ADF中利用勾股定理得(10k)2+(5k)2=102,解得k=$\frac{2\sqrt{5}}{5}$,然后计算矩形ABCD的面积;
(2)如图,作∠ADF的平分线交AF于O点,由于AF平分∠EAD和∠EFD,则点O到四边形AEFD各边的距离相等,这样作OH⊥AD于H,以点O为圆心,OH为半径作⊙O,⊙O为所作,设⊙O的半径为r,易得OH=DH=r,然后证明△AOH∽△AFD,然后利用相似比可计算出r.
解答 解:(1)在Rt△EFC中,∵tan∠FEC=$\frac{FC}{EC}$=$\frac{3}{4}$,
∴设FC=3k,EC=4k,
∴EF=$\sqrt{E{C}^{2}+F{C}^{2}}$=5k,
∵折叠矩形ABCD的一边AD使点D落在BC边上的E处,
∴DF=EF=5k,AD=AE,∠AEF=∠D=90°,
∴DC=DF+CF=5k+3k=8k,
∴AB=CD=8k,
∵∠AEB+∠FEC=90°,∠AEB+∠BAE=90°,
∴∠BAE=∠FEC
在Rt△ABE中,∵tan∠BAE=tan∠FEC=$\frac{BE}{AB}$=$\frac{3}{4}$,
∴BE=6k,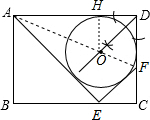
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=10k,
∴AD=10k,
在Rt△ADF中,∵AD2+DF2=AF2,
∴(10k)2+(5k)2=102,解得k=$\frac{2\sqrt{5}}{5}$,
∴矩形ABCD的面积=10k•8k=80•$\frac{4}{5}$=64;
(2)如图,作∠ADF的平分线交AF于O点,作OH⊥AD于H,以点O为圆心,OH为半径作⊙O即可,
设⊙O的半径为r,
∵∠ODH=45°,
∴△OHD为等腰直角三角形,
∴OH=DH=r,
∵OH∥DF,
∴△AOH∽△AFD,
∴$\frac{OH}{DF}$=$\frac{AH}{AD}$,即$\frac{r}{5k}$=$\frac{10k-r}{10k}$,
∴r=$\frac{10}{3}$k=$\frac{10}{3}$×$\frac{2\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{3}$,
即⊙O的半径为$\frac{4\sqrt{5}}{3}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了复杂作图和相似三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(1,-1) | B. | 图象位于第二、四象限 | ||
| C. | 当x<0时,y随x增大而增大 | D. | 图象是中心对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
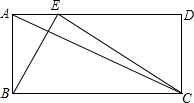 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.
如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com