
【题目】如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.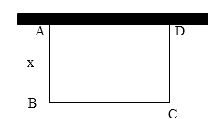
(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
【答案】
(1)
BC=32-2x
(2)
能.
由题知: x(32-2x)=120,
化简整理得(x-6)(x-10)=0,
解得:x1=6,x2=10,
经检验x1=6 ,x2=10都是原方程的解但x1=6时长为20大于墙长,所以不符合题意,舍去,
答:能建成面积为120㎡仓库,此时长为12米,宽为10米.
(3)
不能.
由题知: x(32-2x)=160
化简整理得:x2-16x+80=0,
此时b2-4ac=162-4×1×80=-64, 此方程无解
所以不能建造成面积为160㎡的长方形仓库.
【解析】(1)只做2条宽和1条长,则BC=32-2x;
(2)长方形的面积为 x(32-2x)列出方程求解,并验证答案,长不能大于16米;
(3)列出方程,根据判别式判断方程的解的情况.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
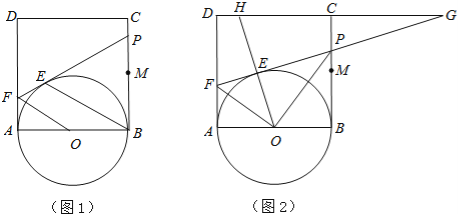
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=Rt∠,直角边AB、BC的长(AB<BC)是方程 ![]() 2-7
2-7 ![]() +12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).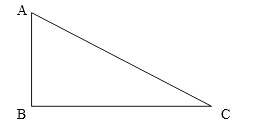
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为 ![]() 时运动时间t的值;
时运动时间t的值;
(3)点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (12分)某地电话拨号入网有两种收费方式,用户可以任选其一:
方法一:计时制:0.05元/分;
方法二:包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)设某用户某月上网的时间为![]() 小时,请你分别写出两种收费方式下该用户应该支付的费用;
小时,请你分别写出两种收费方式下该用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) 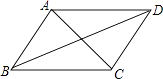
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com