
【题目】在线段、平行四边形、矩形、等腰三角形、正六边形、圆这几个图形中,既是轴对称图形又是中心对称图形的个数是( )
A.2个B.3个C.4个D.5个
科目:初中数学 来源: 题型:
【题目】南海地质勘探队在南沙群岛的一小岛发现很有价值的A,B两种矿石,A矿石大约565吨,B矿石大约500吨,上报公司,要一次性将两种矿石运往冶炼厂,需要不同型号的甲、乙两种货船共30艘,甲货船每艘运费1000元,乙货船每艘运费1200元.
(1)设运送这些矿石的总费用为y元,若使用甲货船x艘,请写出y和x之间的函数关系式;
(2)如果甲货船最多可装A矿石20吨和B矿石15吨,乙货船最多可装A矿石15吨和B矿石25吨,装矿石时按此要求安排甲、乙两种货船,共有几种安排方案?哪种安排方案运费最低并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣。当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;当A、B两点都不在原点时,如图2,点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;
如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;
如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是,数轴上表示-2和-5的两点之间的距离是,数轴上表示1和-3的两点之间的距离是;
(2)数轴上表示x和-1的两点A和B之间的距离是,如果∣AB∣=2,那么x为
(3)当代数式∣x+1∣+∣x-2∣+∣x+3∣取最小值时,相应的x的值是;此时代数式∣x+1∣+∣x-2∣+∣x+3∣的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图5,O为直线AB上一点, ∠AOC=48°,OE平分∠AOC, ∠DOE=90°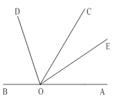
(1)求∠BOE的度数。
(2)试判断OD是否平分∠BOC?试说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com