
 时,求AD的长.
时,求AD的长.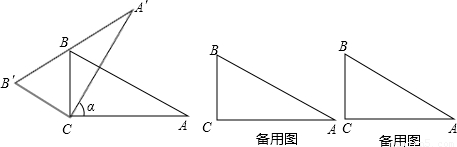
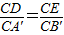 、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得
、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得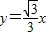 (0<x<2);
(0<x<2);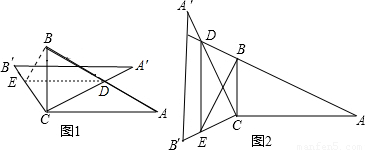 解:(1)在Rt△ABC中,∵∠A=30°,
解:(1)在Rt△ABC中,∵∠A=30°,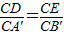 .(1分)
.(1分)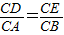 ,(1分)
,(1分)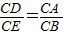 .
.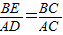 .
.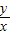 =
=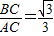 .(1分)
.(1分)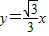 (0<x<2)(2分)
(0<x<2)(2分)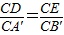 ,
,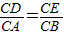 ,
,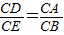 ,
,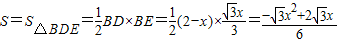 .
.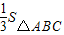 时,
时,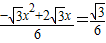 .
.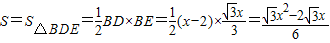 .
.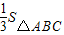 时,
时,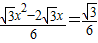 .
.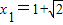 ,
,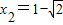 (负值,舍去).
(负值,舍去).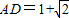 .(2分)
.(2分)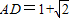 .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源:2011年上海市普陀区中考数学二模试卷(解析版) 题型:解答题
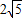 的⊙C与x轴交于A(-1,0)、B(3,0)两点,且点C在x轴的上方.
的⊙C与x轴交于A(-1,0)、B(3,0)两点,且点C在x轴的上方.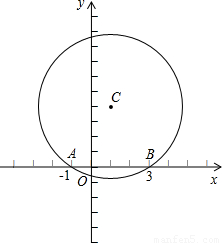
查看答案和解析>>
科目:初中数学 来源:2011年上海市普陀区中考数学二模试卷(解析版) 题型:解答题
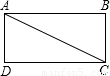
查看答案和解析>>
科目:初中数学 来源:2011年上海市普陀区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2011年上海市普陀区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com