
【题目】如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).(参考数据:sin27°≈0.45,cos27°≈0.90,tan27°≈0.50,![]() ≈1.73)
≈1.73)
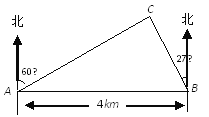
【答案】灯塔C与观测点A的距离为3.6 km.
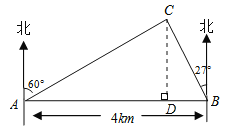
【解析】试题分析:如图,过点C作CD⊥AB,构建直角△ACD和直角△BCD.通过解Rt△BDC得到BD=0.5CD.通过解Rt△ADC得到AD=![]() CD,所以由AB=4km可求得CD的长度.最后通过解Rt△ADC来求AC的长度.
CD,所以由AB=4km可求得CD的长度.最后通过解Rt△ADC来求AC的长度.
试题解析:如图,过点C作CD⊥AB,则∠BCD=27°,∠ACD=60°,
在Rt△BDC中,由tan∠BCD=![]() ,
,
∴BD="CD" tan27°=0.5CD.
在Rt△ADC中,由tan∠ACD=![]()
∴AD=CDtan60°=![]() CD.
CD.
∵AD+BD=![]() CD+0.5CD=4,
CD+0.5CD=4,
∴CD=![]() .
.
在Rt△ADC中,∵∠ACD=60°,
∴∠CAD=30°,
∴AC=2CD=![]() ≈3.6.
≈3.6.
∴灯塔C与观测点A的距离为3.6km.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】图①、图②、图③都是由8个大小完全相同的矩形拼成无重叠、无缝隙的图形,每个小矩形的顶点叫做格点,线段![]() 的端点都在格点上. 仅用无刻度的直尺分别在下列方框内完成作图,保留作图痕迹.
的端点都在格点上. 仅用无刻度的直尺分别在下列方框内完成作图,保留作图痕迹.



(1)在图①中,作线段![]() 的一条垂线
的一条垂线![]() ,点
,点![]() 、
、![]() 在格点上.
在格点上.
(2)在图②、图③中,以![]() 为边,另外两个顶点在格点上,各画一个平行四边形,所画的两个平行四边形不完全重合.
为边,另外两个顶点在格点上,各画一个平行四边形,所画的两个平行四边形不完全重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水,每户每月水费按如下标准收费:月用水量不超过8立方米,按每立方米a元收取;月用水量超过8立方米但不超过14立方米的部分,按每立方米b元收取;月用水量超过14立方米的部分,按每立方米c元收取.下表是某月部分居民的用水量及缴纳水费的数据.
用水量(立方米) | 2.5 | 15 | 6 | 12 | 10.3 | 4.7 | 9 | 17 | 16 |
水费(元) | 5 | 33.4 | 12 | 25.6 | 21.52 | 9.4 | 18.4 | 39.4 | 36.4 |
(1) ①a= _____,b= _____,c= _____;
②若小明家七月份需缴水费31元,则小明家七月份用水 米3;
(2) 该市某用户两个月共用水30立方米,设该用户在其中一个月用水x立方米,请列式表示这两个月该用户应缴纳的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:1,﹣5,|﹣![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]() .
.
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)正整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为________时,△CDF为等腰三角形。
,AD=2,点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F,当BE的长为________时,△CDF为等腰三角形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐![]() 为标准,超过和不足的千克数分别用正、负数来表示,记录如下:
为标准,超过和不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位: |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重 ![]() ;
;
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价1.68元,则出售这20筐白菜一共可卖多少元?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
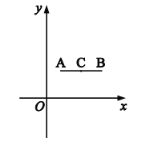
【题目】在平面坐标系![]() 中,已知线段
中,已知线段![]() ,且
,且![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
(1)线段![]() 与
与![]() 轴的位置关系是
轴的位置关系是
(2)求点![]() 的坐标。
的坐标。
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得三角形
,使得三角形![]() 面积为3.若存在,求出点
面积为3.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,锐角△ABC的两条高CD、BE相交于点O,且OB=OC
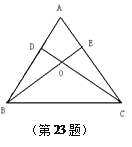
1.求证:△ABC是等腰三角形
2.连结AO,判断AO与BC的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com