
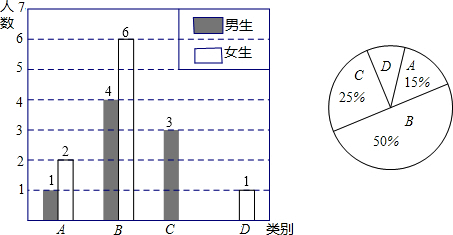
分析 (1)首先根据题意求得:张老师一共调查的学生数为:(1+2)÷15%=20(名);继而求得C类女生有:20×25%-3=2(名),D类男生有:20×(1-15%-25%-50%)-1=1(名);
(2)根据(1),即可补全统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所选两位同学恰好是一位男同学和一位女同学的情况,再利用概率公式即可求得答案.
解答 解:(1)根据题意得:张老师一共调查的学生数为:(1+2)÷15%=20(名);
C类女生有:20×25%-3=2(名),D类男生有:20×(1-15%-25%-50%)-1=1(名);
故答案为:20;2;1;
(2)补全统计图得: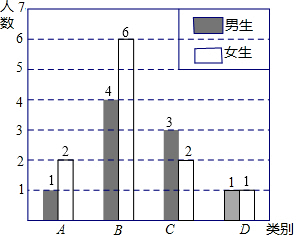
(3)画树状图得: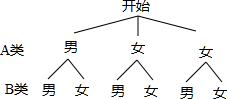
∵共有6种等可能的结果,所选两位同学恰好是一位男同学和一位女同学的有3种情况,
∴所选两位同学恰好是一位男同学和一位女同学的概率是:$\frac{3}{6}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
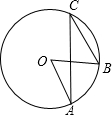 如图,在⊙O中,点A、B、C是圆上的点,连接OA、OB、AC、BC,若∠CAO=20°,∠CBO=50°,∠AOB的度数是( )
如图,在⊙O中,点A、B、C是圆上的点,连接OA、OB、AC、BC,若∠CAO=20°,∠CBO=50°,∠AOB的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
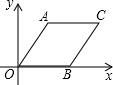 菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-3,1)或(3,-1).
菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-3,1)或(3,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1<x≤1 | B. | -1<x≤1 | C. | x≥1 | D. | x>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com