
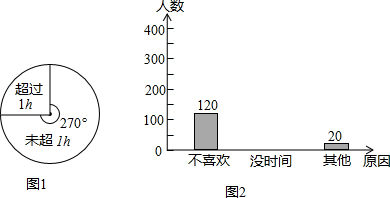
分析 (1)先求出未超1h的人数,减去不喜欢和其他原因的即可求出“没时间”的人数,再补全频数分布直方图;
(2)根据扇形统计图可以知道每天锻炼超过1h的百分比,然后乘以18万即可得到2015年全市中小学生每天锻炼超过1h的约有的人数;
(3)设2015年至2017年锻炼未超过1h人数的年平均降低的百分率为x,由于计划2017年全市中小学生每天锻炼未超过1h的人数减少到8.64万人,由此可以列出方程18×0.75(1-x)2=8.64,解方程即可求出2015年至2017年锻炼未超过1h人数的年平均降低的百分率.
解答 解:(1)∵随机调查了340名学生,
∴锻炼未超过1h的中小学生有340×$\frac{270}{360}$=255人,
又∵不喜欢的人数和其他的人数分别是120和20,
∴“没时间”的人数为255-120-20=115人,
频数分布直方图如图所示: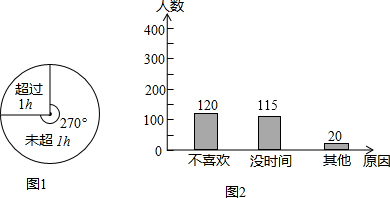
(2)根据扇形统计图知道:
每天锻炼超过1h的百分比为18×$\frac{360-270}{360}$=4.5万人.
故估计2015年全市中小学生每天锻炼超过1h的约有4.5万人;
(3)设2015年至2017年锻炼未超过1h人数的年平均降低的百分率为x.
由题意得:18×0.75(1-x)2=8.64,
解得x=0.2,x=1.8(舍去).
答:2015年至2017年锻炼未超过1h人数的年平均降低的百分率为20%.
故答案为:115;4.5.
点评 此题比较复杂,既考查读频数分布直方图的能力和利用统计图获取信息的能力,也考查增长率的问题.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
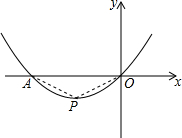 已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点P的坐标为(-$\sqrt{3}$,-1)
已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点P的坐标为(-$\sqrt{3}$,-1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
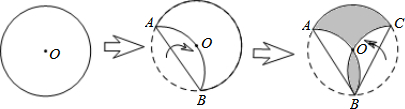
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
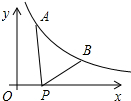 如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )| A. | (0.5,0) | B. | (1,0) | C. | (1.5,0) | D. | (2.5,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
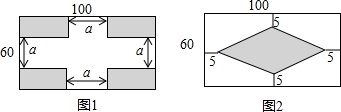
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2015次翻转之后,点B的坐标是(4031,$\sqrt{3}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2015次翻转之后,点B的坐标是(4031,$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
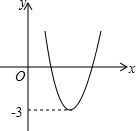 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+1=0的根的情况是( )
已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+1=0的根的情况是( )| A. | 无实数根 | B. | 有两个相等实数根 | ||
| C. | 有两个异号实数根 | D. | 有两个同号不等实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com