
【题目】设△ABC的内角A、B、C的对边长分别为a、b、c.设S为△ABC的面积,满足S= ![]() (a2+c2﹣b2). (Ⅰ)求B;
(a2+c2﹣b2). (Ⅰ)求B;
(Ⅱ)若b= ![]() ,求(
,求( ![]() ﹣1)a+2c的最大值.
﹣1)a+2c的最大值.
【答案】解:(Ⅰ)∵S= ![]() acsinB,cosB=
acsinB,cosB= ![]() 即a2+c2﹣b2=2accosB, ∴S=
即a2+c2﹣b2=2accosB, ∴S= ![]() (a2+c2﹣b2)变形得:
(a2+c2﹣b2)变形得: ![]() acsinB=
acsinB= ![]() ×2accosB,
×2accosB,
整理得:tanB= ![]() ,
,
又0<B<π,
∴B= ![]() ,
,
(Ⅱ)∵A+B+C=π,
∴0<A< ![]() ,
,
由正弦定理知a= ![]() =
=  =2sinA,
=2sinA,
c= ![]() =2sin(
=2sin( ![]() ﹣A),
﹣A),
∴( ![]() ﹣1)a+2c=2(
﹣1)a+2c=2( ![]() ﹣1)sinA+4sin(
﹣1)sinA+4sin( ![]() ﹣A)=2
﹣A)=2 ![]() sinA+2
sinA+2 ![]() cosA=2
cosA=2 ![]() sin(A+
sin(A+ ![]() )≤2
)≤2 ![]() ,
,
当且仅当A= ![]() 时取最大值,
时取最大值,
故( ![]() ﹣1)a+2c的最大值为2
﹣1)a+2c的最大值为2 ![]()
【解析】(Ⅰ)利用三角形的面积公式表示出S,利用余弦定理表示出cosB,代入已知等式求出tanB的值,即可求出B,(Ⅱ)先求出A的范围,再根据正弦定理表示出a,c,根据两角和差的正弦公式,正弦函数的图象和性质即可求出最大值


科目:初中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(a∈R)与函数 ![]() 有公共切线. (Ⅰ)求a的取值范围;
有公共切线. (Ⅰ)求a的取值范围;
(Ⅱ)若不等式xf(x)+e>2﹣a对于x>0的一切值恒成立,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知斜三棱柱ABC﹣A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2 ![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C. 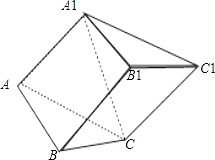
(1)求侧棱A1A与底面ABC所成角的大小;
(2)求侧面A1ABB1与底面ABC所成二面角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD= ![]() ,DC=SD=2,点M在侧棱SC上,∠ABM=60°.
,DC=SD=2,点M在侧棱SC上,∠ABM=60°. 
(Ⅰ)证明:M是侧棱SC的中点;
(Ⅱ)求二面角S﹣AM﹣B的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是π,将f(x)图象向左平移 ![]() 个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
A.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为 ![]() . (Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
. (Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换 ![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
查看答案和解析>>
科目:初中数学 来源: 题型:
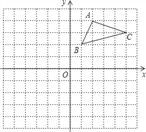
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)在直角坐标系中画出△ABC关于x轴的对称图形△A1B1C1;
(2)在直角坐标系中将△ABC向左平移4个单位长度得△A2B2C2,画出△A2B2C2;
(3)若点D(m,n)在△ABC的边AC上,请分别写出△A1B1C1和△A2B2C2 的对应点D1和D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的周长为12,AB,AC边的中点分别为F1(﹣1,0)和F2(1,0),点M为BC边的中点.
(1)求点M的轨迹方程;
(2)设点M的轨迹为曲线T,直线MF1与曲线T另一个交点为N,线段MF2中点为E,记S=S ![]() +S
+S ![]() ,求S的最大值.
,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2∥l3 , 等腰直角△ABC的三个顶点A,B,C分别在l1 , l2 , l3上,若∠ACB=90°,l1 , l2的距离为1,l2 , l3的距离为3,求: 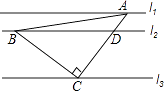
(1)线段AB的长;
(2)![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com